"""
(Can be view as
[html](http://menzies.us/cs472/?niching) or [raw
Python](http://unbox.org/open/trunk/472/14/spring/src/where.py).)
How to Find Niche Solutions
===========================
### Why Niche?
When exploring complex multi-objective surfaces, it
is trite to summarize that space with one number
such _max distance from hell_ (where _hell_ is the
point in objective space where all goals have their
worse values). For example, all the following points
have the same _distance from hell_, but they reflect
very different solutions:
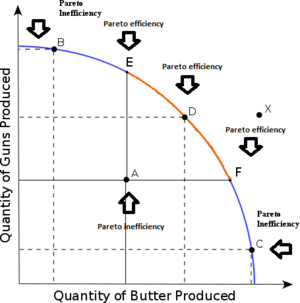 A better way to do it is _niching_; i.e. generate
the Pareto frontier, then cluster that frontier and
report a (small) number of random samples from each
cluster. In this approach, "distance from hell" can
still be used internally to guide a quick search for
places to expand the frontier. But after that, we
can isolate interesting different parts of the
solution space.
For example, when exploring options for configuring
London Ambulances, Veerappa and Letier use optimization to
reject thousands of options (shown in red) in order
to isolate clusters of better solutions C1,C2,etc
(shown in green). In this example, the goal is to
minimize X and maximize Y .
A better way to do it is _niching_; i.e. generate
the Pareto frontier, then cluster that frontier and
report a (small) number of random samples from each
cluster. In this approach, "distance from hell" can
still be used internally to guide a quick search for
places to expand the frontier. But after that, we
can isolate interesting different parts of the
solution space.
For example, when exploring options for configuring
London Ambulances, Veerappa and Letier use optimization to
reject thousands of options (shown in red) in order
to isolate clusters of better solutions C1,C2,etc
(shown in green). In this example, the goal is to
minimize X and maximize Y .
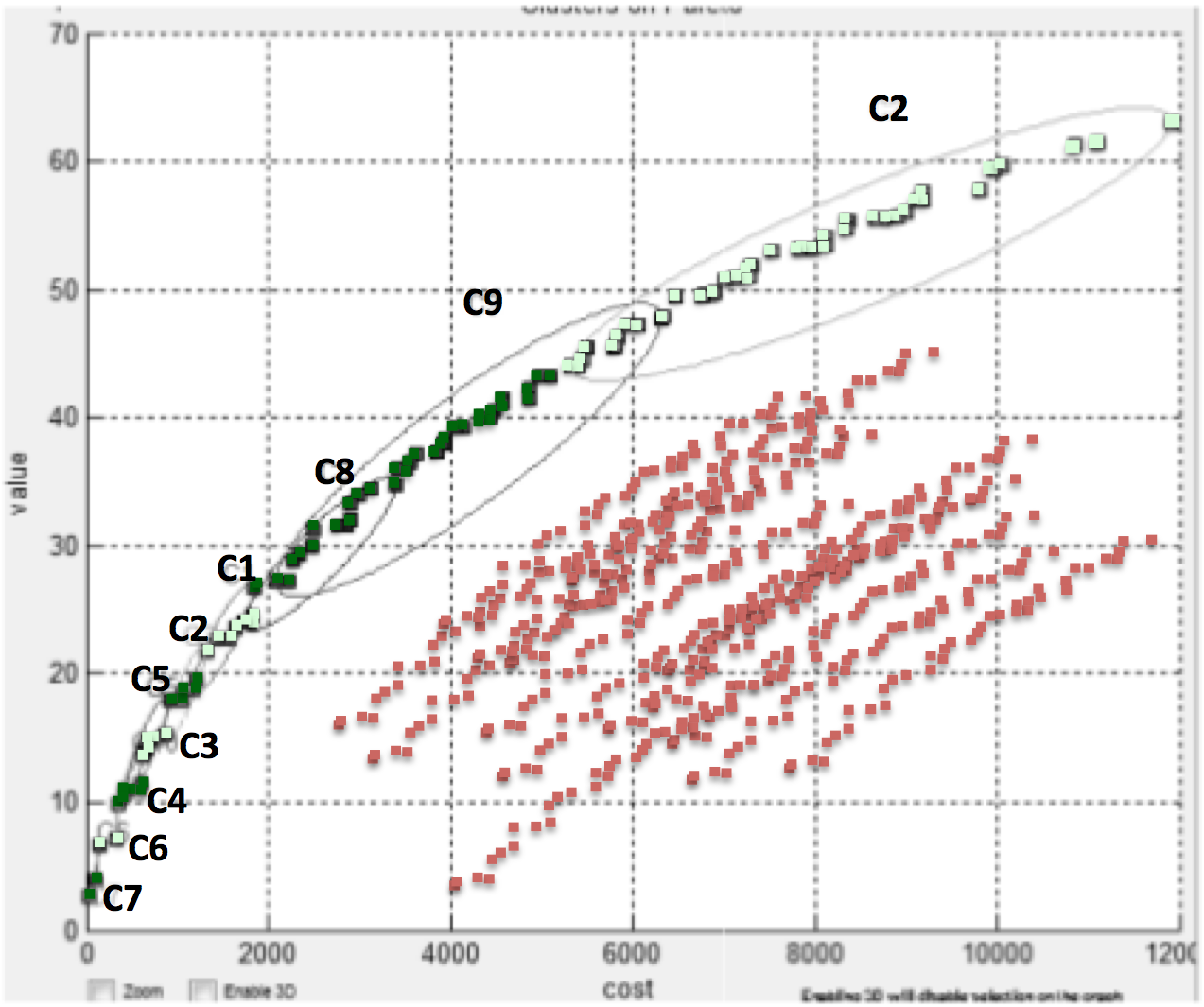 (REF: V. Veerappa and E. Letier, "Understanding
clusters of optimal solutions in multi-objective
decision problems, in RE' 2011, Trento, Italy,
2011, pp. 89-98.)
### What is a Niche?
According to Deb and Goldberg (1989) _a niche is
viewed as an organism's task in the environment and
a species is a collection of organisms with similar
features_.
+ REF: Kalyanmoy Deb and David
E. Goldberg. 1989. [An Investigation of Niche and
Species Formation in Genetic Function
Optimization](http://goo.gl/oLIxo1). In
Proceedings of the 3rd International Conference on
Genetic Algorithms, J. David Schaffer (Ed.). Morgan
Kaufmann Publishers Inc., San Francisco, CA, USA,
42-50.
Their definition seems to suggest that niching means
clustering in objective space and species are the
things that form in each such cluster. Strange to
say, some of their examples report _niches_ using
decision space so all we can say is that it is an
engineering decision whether or not you _niche_ in
objective space or _niche_ in decision space. Note
that the above example from Veerappa and Letier
build niches in objective space while my code, shown
below, builds niches in decision space.
### How to Niche?
In any case, in decision or objective space, the
open issue is now to fun the niches? A naive
approach is to compute distances between all
individuals. This can be very slow, especially if
this calculation is called repeatedly deep inside
the inner-most loop of a program. In practice, any
program working with distance spends most of its
time computing those measures. Various proposals
exist to prevent that happening:
+ _Canopy clustering_: McCallum, A.; Nigam, K.; and
Ungar L.H. (2000) [ Efficient Clustering of High
Dimensional Data Sets with Application to
Reference Matching](http://goo.gl/xwIzN),
Proceedings of the sixth ACM SIGKDD international
conference on Knowledge discovery and data
mining, 169-178
+ _Incremental stochastic k-means_ [Web-Scale
K-Means Clustering](http://goo.gl/V8BQs),
WWW 2010, April 26-30, 2010, Raleigh, North
Carolina, USA.
+ _Triangle inequality tricks_ (which work very well
indeed) [Making k-means Even Faster](http://goo.gl/hk3Emn).
G Hamerly - 2010 SIAM International Conference on
Data Mining.
My own favorite trick is WHERE, shown below. It uses
a data mining trick to recursively divide the space
of decisions in two, then four, then eight,
etc. REF: [Local vs. global lessons for defect
prediction and effort
estimation](http://menzies.us/pdf/12gense.pdf) T
Menzies, A Butcher, D Cok, A Marcus, L Layman, F
Shull, B Turhan, IEEE Transactions on Software
Engineering 29 (6), 822-834, 2012.
WHERE uses a linear-time trick (called the FastMap
heuristic) to find two distant solutions- these are
the _poles_ called _west_ and _east_. Note that the
following takes only _O(2N)_ distance calculations:
"""
def fastmap(m,data):
"Divide data into two using distance to two distant items."
one = any(data) # 1) pick anything
west = furthest(m,one,data) # 2) west is as far as you can go from anything
east = furthest(m,west,data) # 3) east is as far as you can go from west
c = dist(m,west,east)
# now find everyone's distance
xsum, lst = 0.0,[]
for one in data:
a = dist(m,one,west)
b = dist(m,one,east)
x = (a*a + c*c - b*b)/(2*c) # cosine rule
xsum += x
lst += [(x,one)]
# now cut data according to the mean distance
cut, wests, easts = xsum/len(data), [], []
for x,one in lst:
where = wests if x < cut else easts
where += [one]
return wests,west, easts,east
"""
In the above:
+ _m_ is some model that generates candidate
solutions that we wish to niche.
+ _(west,east)_ are not _the_ most distant points
(that would require _N*N) distance
calculations). But they are at least very distant
to each other.
This code needs some helper functions. _Dist_ uses
the standard Euclidean measure. Note that you tune
what it uses to define the niches (decisions or
objectives) using the _what_ parameter:
"""
def dist(m,i,j,
what = lambda x: x.dec):
"Euclidean distance 0 <= d <= 1 between decisions"
d1,d2 = what(i), what(j)
n = len(d1)
deltas = 0
for d in range(n):
n1 = norm(m, d, d1[d])
n2 = norm(m, d, d2[d])
inc = (n1-n2)**2
deltas += inc
return deltas**0.5 / n**0.5
"""
The _Dist_ function normalizes all the raw values zero to one.
"""
def norm(m,x,n) :
"Normalizes value n on variable x within model m 0..1"
return (n - lo(m,x)) / (hi(m,x) - lo(m,x) + 0.0001)
"""
Now we can define _furthest_:
"""
def furthest(m,i,all,
init = 0,
better = lambda x,y: x>y):
"find which of all is furthest from 'i'"
out,d= i,init
for j in all:
if not i == j:
tmp = dist(m,i,j)
if better(tmp,d): out,d = j,tmp
return out
"""
WHERE finds everyone's else's distance from the poles
and divide the data on the mean point of those
distances. This all stops if:
+ Any division has _tooFew_ solutions (say,
less than _sqrt_ of the total number of
solutions).
+ Something has gone horribly wrong and you are
recursing _tooDeep_
This code is controlled by a set of _slots_. For
example, if _slots.pruning_ is true, we may ignore
some sub-tree (this process is discussed, later on).
Also, if _slots.verbose_ is true, the _show_
function prints out a little tree showing the
progress (and to print indents in that tree, we use
the string _slots.b4_). For example, here's WHERE
dividing 100 solutions:
100
|.. 50
|.. |.. 25
|.. |.. |.. 11
|.. |.. |.. |.. 6.
|.. |.. |.. |.. 5.
|.. |.. |.. 14
|.. |.. |.. |.. 6.
|.. |.. |.. |.. 8.
|.. |.. 25
|.. |.. |.. 12
|.. |.. |.. |.. 5.
|.. |.. |.. |.. 7.
|.. |.. |.. 13
|.. |.. |.. |.. 5.
|.. |.. |.. |.. 8.
|.. 50
|.. |.. 25
|.. |.. |.. 13
|.. |.. |.. |.. 7.
|.. |.. |.. |.. 6.
|.. |.. |.. 12
|.. |.. |.. |.. 5.
|.. |.. |.. |.. 7.
|.. |.. 25
|.. |.. |.. 11
|.. |.. |.. |.. 5.
|.. |.. |.. |.. 6.
|.. |.. |.. 14
|.. |.. |.. |.. 7.
|.. |.. |.. |.. 7.
Here's the slots:
"""
class Slots():
"Place to read/write named slots."
id = -1
def __init__(i,**d) :
i.id = Slots.id = Slots.id + 1
i.override(d)
def override(i,d): i.__dict__.update(d); return i
def __eq__(i,j) : return i.id == j.id
def __ne__(i,j) : return i.id != j.id
def __repr__(i) : return '{' + showd(i.__dict__) + '}'
def where0(**other):
return Slots(minSize = 10, # min leaf size
depthMin= 2, # no pruning till this depth
depthMax= 10, # max tree depth
wriggle = 0.2, # min difference of 'better'
prune = True, # pruning enabled?
b4 = '|.. ', # indent string
verbose = False, # show trace info?
hedges = 0.38 # strict=0.38,relax=0.17
).override(other)
"""
WHERE returns clusters, where each cluster contains
multiple solutions.
"""
def where(m,data,slots=where0()):
out = []
where1(m,data,slots,0,out)
return out
def where1(m, data, slots, lvl, out):
def tooDeep(): return lvl > slots.depthMax
def tooFew() : return len(data) < slots.minSize
def show(suffix):
if slots.verbose:
print slots.b4*lvl + str(len(data)) + suffix
if tooDeep() or tooFew():
show(".")
out += [data]
else:
show("")
wests,west, easts,east = fastmap(m,data)
goLeft, goRight = maybePrune(m,slots,lvl,west,east)
if goLeft:
where1(m, wests, slots, lvl+1, out)
if goRight:
where1(m, easts, slots, lvl+1, out)
"""
Is this useful? Well, in the following experiment, I
clustered 32, 64, 128, 256 individuals using WHERE or
a dumb greedy approach called GAC that (a) finds
everyone's closest neighbor; (b) combines each such
pair into a super-node; (c) then repeats
(recursively) for the super-nodes.
(REF: V. Veerappa and E. Letier, "Understanding
clusters of optimal solutions in multi-objective
decision problems, in RE' 2011, Trento, Italy,
2011, pp. 89-98.)
### What is a Niche?
According to Deb and Goldberg (1989) _a niche is
viewed as an organism's task in the environment and
a species is a collection of organisms with similar
features_.
+ REF: Kalyanmoy Deb and David
E. Goldberg. 1989. [An Investigation of Niche and
Species Formation in Genetic Function
Optimization](http://goo.gl/oLIxo1). In
Proceedings of the 3rd International Conference on
Genetic Algorithms, J. David Schaffer (Ed.). Morgan
Kaufmann Publishers Inc., San Francisco, CA, USA,
42-50.
Their definition seems to suggest that niching means
clustering in objective space and species are the
things that form in each such cluster. Strange to
say, some of their examples report _niches_ using
decision space so all we can say is that it is an
engineering decision whether or not you _niche_ in
objective space or _niche_ in decision space. Note
that the above example from Veerappa and Letier
build niches in objective space while my code, shown
below, builds niches in decision space.
### How to Niche?
In any case, in decision or objective space, the
open issue is now to fun the niches? A naive
approach is to compute distances between all
individuals. This can be very slow, especially if
this calculation is called repeatedly deep inside
the inner-most loop of a program. In practice, any
program working with distance spends most of its
time computing those measures. Various proposals
exist to prevent that happening:
+ _Canopy clustering_: McCallum, A.; Nigam, K.; and
Ungar L.H. (2000) [ Efficient Clustering of High
Dimensional Data Sets with Application to
Reference Matching](http://goo.gl/xwIzN),
Proceedings of the sixth ACM SIGKDD international
conference on Knowledge discovery and data
mining, 169-178
+ _Incremental stochastic k-means_ [Web-Scale
K-Means Clustering](http://goo.gl/V8BQs),
WWW 2010, April 26-30, 2010, Raleigh, North
Carolina, USA.
+ _Triangle inequality tricks_ (which work very well
indeed) [Making k-means Even Faster](http://goo.gl/hk3Emn).
G Hamerly - 2010 SIAM International Conference on
Data Mining.
My own favorite trick is WHERE, shown below. It uses
a data mining trick to recursively divide the space
of decisions in two, then four, then eight,
etc. REF: [Local vs. global lessons for defect
prediction and effort
estimation](http://menzies.us/pdf/12gense.pdf) T
Menzies, A Butcher, D Cok, A Marcus, L Layman, F
Shull, B Turhan, IEEE Transactions on Software
Engineering 29 (6), 822-834, 2012.
WHERE uses a linear-time trick (called the FastMap
heuristic) to find two distant solutions- these are
the _poles_ called _west_ and _east_. Note that the
following takes only _O(2N)_ distance calculations:
"""
def fastmap(m,data):
"Divide data into two using distance to two distant items."
one = any(data) # 1) pick anything
west = furthest(m,one,data) # 2) west is as far as you can go from anything
east = furthest(m,west,data) # 3) east is as far as you can go from west
c = dist(m,west,east)
# now find everyone's distance
xsum, lst = 0.0,[]
for one in data:
a = dist(m,one,west)
b = dist(m,one,east)
x = (a*a + c*c - b*b)/(2*c) # cosine rule
xsum += x
lst += [(x,one)]
# now cut data according to the mean distance
cut, wests, easts = xsum/len(data), [], []
for x,one in lst:
where = wests if x < cut else easts
where += [one]
return wests,west, easts,east
"""
In the above:
+ _m_ is some model that generates candidate
solutions that we wish to niche.
+ _(west,east)_ are not _the_ most distant points
(that would require _N*N) distance
calculations). But they are at least very distant
to each other.
This code needs some helper functions. _Dist_ uses
the standard Euclidean measure. Note that you tune
what it uses to define the niches (decisions or
objectives) using the _what_ parameter:
"""
def dist(m,i,j,
what = lambda x: x.dec):
"Euclidean distance 0 <= d <= 1 between decisions"
d1,d2 = what(i), what(j)
n = len(d1)
deltas = 0
for d in range(n):
n1 = norm(m, d, d1[d])
n2 = norm(m, d, d2[d])
inc = (n1-n2)**2
deltas += inc
return deltas**0.5 / n**0.5
"""
The _Dist_ function normalizes all the raw values zero to one.
"""
def norm(m,x,n) :
"Normalizes value n on variable x within model m 0..1"
return (n - lo(m,x)) / (hi(m,x) - lo(m,x) + 0.0001)
"""
Now we can define _furthest_:
"""
def furthest(m,i,all,
init = 0,
better = lambda x,y: x>y):
"find which of all is furthest from 'i'"
out,d= i,init
for j in all:
if not i == j:
tmp = dist(m,i,j)
if better(tmp,d): out,d = j,tmp
return out
"""
WHERE finds everyone's else's distance from the poles
and divide the data on the mean point of those
distances. This all stops if:
+ Any division has _tooFew_ solutions (say,
less than _sqrt_ of the total number of
solutions).
+ Something has gone horribly wrong and you are
recursing _tooDeep_
This code is controlled by a set of _slots_. For
example, if _slots.pruning_ is true, we may ignore
some sub-tree (this process is discussed, later on).
Also, if _slots.verbose_ is true, the _show_
function prints out a little tree showing the
progress (and to print indents in that tree, we use
the string _slots.b4_). For example, here's WHERE
dividing 100 solutions:
100
|.. 50
|.. |.. 25
|.. |.. |.. 11
|.. |.. |.. |.. 6.
|.. |.. |.. |.. 5.
|.. |.. |.. 14
|.. |.. |.. |.. 6.
|.. |.. |.. |.. 8.
|.. |.. 25
|.. |.. |.. 12
|.. |.. |.. |.. 5.
|.. |.. |.. |.. 7.
|.. |.. |.. 13
|.. |.. |.. |.. 5.
|.. |.. |.. |.. 8.
|.. 50
|.. |.. 25
|.. |.. |.. 13
|.. |.. |.. |.. 7.
|.. |.. |.. |.. 6.
|.. |.. |.. 12
|.. |.. |.. |.. 5.
|.. |.. |.. |.. 7.
|.. |.. 25
|.. |.. |.. 11
|.. |.. |.. |.. 5.
|.. |.. |.. |.. 6.
|.. |.. |.. 14
|.. |.. |.. |.. 7.
|.. |.. |.. |.. 7.
Here's the slots:
"""
class Slots():
"Place to read/write named slots."
id = -1
def __init__(i,**d) :
i.id = Slots.id = Slots.id + 1
i.override(d)
def override(i,d): i.__dict__.update(d); return i
def __eq__(i,j) : return i.id == j.id
def __ne__(i,j) : return i.id != j.id
def __repr__(i) : return '{' + showd(i.__dict__) + '}'
def where0(**other):
return Slots(minSize = 10, # min leaf size
depthMin= 2, # no pruning till this depth
depthMax= 10, # max tree depth
wriggle = 0.2, # min difference of 'better'
prune = True, # pruning enabled?
b4 = '|.. ', # indent string
verbose = False, # show trace info?
hedges = 0.38 # strict=0.38,relax=0.17
).override(other)
"""
WHERE returns clusters, where each cluster contains
multiple solutions.
"""
def where(m,data,slots=where0()):
out = []
where1(m,data,slots,0,out)
return out
def where1(m, data, slots, lvl, out):
def tooDeep(): return lvl > slots.depthMax
def tooFew() : return len(data) < slots.minSize
def show(suffix):
if slots.verbose:
print slots.b4*lvl + str(len(data)) + suffix
if tooDeep() or tooFew():
show(".")
out += [data]
else:
show("")
wests,west, easts,east = fastmap(m,data)
goLeft, goRight = maybePrune(m,slots,lvl,west,east)
if goLeft:
where1(m, wests, slots, lvl+1, out)
if goRight:
where1(m, easts, slots, lvl+1, out)
"""
Is this useful? Well, in the following experiment, I
clustered 32, 64, 128, 256 individuals using WHERE or
a dumb greedy approach called GAC that (a) finds
everyone's closest neighbor; (b) combines each such
pair into a super-node; (c) then repeats
(recursively) for the super-nodes.
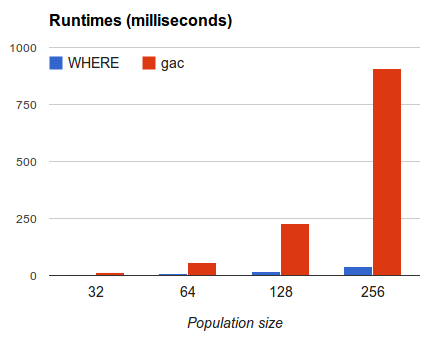 WHERE is _much_ faster than GAC since it builds
a tree of cluster of height log(N) by, at each
step, making only O(2N) calls to FastMap.
### Experimental Extensions
Lately I've been experimenting with a system that
prunes as it divides the data. GALE checks for
domination between the poles and ignores data in
halves with a dominated pole. This means that for
_N_ solutions we only ever have to evaluate
_2*log(N)_ of them- which is useful if each
evaluation takes a long time.
The niches found in this way
contain non-dominated poles; i.e. they are
approximations to the Pareto frontier.
Preliminary results show that this is a useful
approach but you should treat those results with a
grain of salt.
In any case, this code supports that pruning as an
optional extra (and is enabled using the
_slots.pruning_ flag). In summary, this code says if
the scores for the poles are more different that
_slots.wriggle_ and one pole has a better score than
the other, then ignore the other pole.
"""
def maybePrune(m,slots,lvl,west,east):
"Usually, go left then right, unless dominated."
goLeft, goRight = True,True # default
if slots.prune and lvl >= slots.depthMin:
sw = scores(m, west)
se = scores(m, east)
if abs(sw - se) > slots.wriggle: # big enough to consider
if se > sw: goLeft = False # no left
if sw > se: goRight = False # no right
return goLeft, goRight
"""
Note that I do not allow pruning until we have
descended at least _slots.depthMin_ into the tree.
Support Code
------------
### Dull, low-level stuff
"""
import sys,math,random
sys.dont_write_bytecode = True
def go(f):
"A decorator that runs code at load time."
print "\n# ---|", f.__name__,"|-----------------"
if f.__doc__: print "#", f.__doc__
f()
# random stuff
by = lambda x: random.uniform(0,x)
seed = random.seed
any = random.choice
# pretty-prints for list
def gs(lst) : return [g(x) for x in lst]
def g(x) : return float('%g' % x)
"""
### More interesting, low-level stuff
"""
def timing(f,repeats=10):
"How long does 'f' take to run?"
import time
time1 = time.clock()
for _ in range(repeats):
f()
return (time.clock() - time1)*1.0/repeats
def showd(d):
"Pretty print a dictionary."
def one(k,v):
if isinstance(v,list):
v = gs(v)
if isinstance(v,float):
return ":%s %g" % (k,v)
return ":%s %s" % (k,v)
return ' '.join([one(k,v) for k,v in
sorted(d.items())
if not "_" in k])
class Num:
"An Accumulator for numbers"
def __init__(i): i.n = i.m2 = i.mu = 0.0
def s(i) : return (i.m2/(i.n - 1))**0.5
def __add__(i,x):
i.n += 1
delta = x - i.mu
i.mu += delta*1.0/i.n
i.m2 += delta*(x - i.mu)
"""
### Model-specific Stuff
WHERE talks to models via the the following model-specific functions.
Here, we must invent some made-up model that builds
individuals with 4 decisions and 3 objectives.
In practice, you would **start** here to build hooks from WHERE into your model
(which is the **m** passed in to these functions).
"""
def decisions(m) : return [0,1,2,3,4]
def objectives(m): return [0,1,2,3]
def lo(m,x) : return 0.0
def hi(m,x) : return 1.0
def w(m,o) : return 1 # min,max is -1,1
def score(m, individual):
d, o = individual.dec, individual.obj
o[0] = d[0] * d[1]
o[1] = d[2] ** d[3]
o[2] = 2.0*d[3]*d[4] / (d[3] + d[4])
o[3] = d[2]/(1 + math.e**(-1*d[2]))
individual.changed = True
"""
The call to
### Model-general stuff
Using the model-specific stuff, WHERE defines some
useful general functions.
"""
def some(m,x) :
"with variable x of model m, pick one value at random"
return lo(m,x) + by(hi(m,x) - lo(m,x))
def candidate(m):
"Return an unscored individual."
return Slots(changed = True,
scores=None,
obj = [None] * len(objectives(m)),
dec = [some(m,d)
for d in decisions(m)])
def scores(m,t):
"Score an individual."
if t.changed:
score(m,t)
new, n = 0, 0
for o in objectives(m):
x = t.obj[o]
n += 1
tmp = norm(m,o,x)**2
if w(m,o) < 0:
tmp = 1 - tmp
new += tmp
t.scores = (new**0.5)*1.0 / (n**0.5)
t.changed = False
return t.scores
"""
### Demo stuff
To run these at load time, add _@go_ (uncommented) on the line before.
Checks that we can find lost and distant things:
"""
@go
def _distances():
def closest(m,i,all):
return furthest(m,i,all,10**32,lambda x,y: x < y)
random.seed(1)
m = "any"
pop = [candidate(m) for _ in range(4)]
for i in pop:
j = closest(m,i,pop)
k = furthest(m,i,pop)
print "\n",\
gs(i.dec), g(scores(m,i)),"\n",\
gs(j.dec),"closest ", g(dist(m,i,j)),"\n",\
gs(k.dec),"furthest", g(dist(m,i,k))
print i
"""
A standard call to WHERE, pruning disabled:
"""
@go
def _where():
random.seed(1)
m, max, pop, kept = "model",100, [], Num()
for _ in range(max):
one = candidate(m)
kept + scores(m,one)
pop += [one]
slots = where0(verbose = True,
minSize = max**0.5,
prune = False,
wriggle = 0.3*kept.s())
n=0
for leaf in where(m, pop, slots):
n += len(leaf)
print n,slots
"""
Compares WHERE to GAC:
"""
@go
def _whereTiming():
def allPairs(data):
n = 8.0/3*(len(data)**2 - 1) #numevals WHERE vs GAC
for _ in range(int(n+0.5)):
d1 = any(data)
d2 = any(data)
dist("M",d1,d2)
random.seed(1)
for max in [32,64,128,256]:
m, pop, kept = "model",[], Num()
for _ in range(max):
one = candidate(m)
kept + scores(m,one)
pop += [one]
slots = where0(verbose = False,
minSize = 2, # emulate GAC
depthMax=1000000,
prune = False,
wriggle = 0.3*kept.s())
t1 = timing(lambda : where(m, pop, slots),10)
t2 = timing(lambda : allPairs(pop),10)
print max,t1,t2, int(100*t2/t1)
WHERE is _much_ faster than GAC since it builds
a tree of cluster of height log(N) by, at each
step, making only O(2N) calls to FastMap.
### Experimental Extensions
Lately I've been experimenting with a system that
prunes as it divides the data. GALE checks for
domination between the poles and ignores data in
halves with a dominated pole. This means that for
_N_ solutions we only ever have to evaluate
_2*log(N)_ of them- which is useful if each
evaluation takes a long time.
The niches found in this way
contain non-dominated poles; i.e. they are
approximations to the Pareto frontier.
Preliminary results show that this is a useful
approach but you should treat those results with a
grain of salt.
In any case, this code supports that pruning as an
optional extra (and is enabled using the
_slots.pruning_ flag). In summary, this code says if
the scores for the poles are more different that
_slots.wriggle_ and one pole has a better score than
the other, then ignore the other pole.
"""
def maybePrune(m,slots,lvl,west,east):
"Usually, go left then right, unless dominated."
goLeft, goRight = True,True # default
if slots.prune and lvl >= slots.depthMin:
sw = scores(m, west)
se = scores(m, east)
if abs(sw - se) > slots.wriggle: # big enough to consider
if se > sw: goLeft = False # no left
if sw > se: goRight = False # no right
return goLeft, goRight
"""
Note that I do not allow pruning until we have
descended at least _slots.depthMin_ into the tree.
Support Code
------------
### Dull, low-level stuff
"""
import sys,math,random
sys.dont_write_bytecode = True
def go(f):
"A decorator that runs code at load time."
print "\n# ---|", f.__name__,"|-----------------"
if f.__doc__: print "#", f.__doc__
f()
# random stuff
by = lambda x: random.uniform(0,x)
seed = random.seed
any = random.choice
# pretty-prints for list
def gs(lst) : return [g(x) for x in lst]
def g(x) : return float('%g' % x)
"""
### More interesting, low-level stuff
"""
def timing(f,repeats=10):
"How long does 'f' take to run?"
import time
time1 = time.clock()
for _ in range(repeats):
f()
return (time.clock() - time1)*1.0/repeats
def showd(d):
"Pretty print a dictionary."
def one(k,v):
if isinstance(v,list):
v = gs(v)
if isinstance(v,float):
return ":%s %g" % (k,v)
return ":%s %s" % (k,v)
return ' '.join([one(k,v) for k,v in
sorted(d.items())
if not "_" in k])
class Num:
"An Accumulator for numbers"
def __init__(i): i.n = i.m2 = i.mu = 0.0
def s(i) : return (i.m2/(i.n - 1))**0.5
def __add__(i,x):
i.n += 1
delta = x - i.mu
i.mu += delta*1.0/i.n
i.m2 += delta*(x - i.mu)
"""
### Model-specific Stuff
WHERE talks to models via the the following model-specific functions.
Here, we must invent some made-up model that builds
individuals with 4 decisions and 3 objectives.
In practice, you would **start** here to build hooks from WHERE into your model
(which is the **m** passed in to these functions).
"""
def decisions(m) : return [0,1,2,3,4]
def objectives(m): return [0,1,2,3]
def lo(m,x) : return 0.0
def hi(m,x) : return 1.0
def w(m,o) : return 1 # min,max is -1,1
def score(m, individual):
d, o = individual.dec, individual.obj
o[0] = d[0] * d[1]
o[1] = d[2] ** d[3]
o[2] = 2.0*d[3]*d[4] / (d[3] + d[4])
o[3] = d[2]/(1 + math.e**(-1*d[2]))
individual.changed = True
"""
The call to
### Model-general stuff
Using the model-specific stuff, WHERE defines some
useful general functions.
"""
def some(m,x) :
"with variable x of model m, pick one value at random"
return lo(m,x) + by(hi(m,x) - lo(m,x))
def candidate(m):
"Return an unscored individual."
return Slots(changed = True,
scores=None,
obj = [None] * len(objectives(m)),
dec = [some(m,d)
for d in decisions(m)])
def scores(m,t):
"Score an individual."
if t.changed:
score(m,t)
new, n = 0, 0
for o in objectives(m):
x = t.obj[o]
n += 1
tmp = norm(m,o,x)**2
if w(m,o) < 0:
tmp = 1 - tmp
new += tmp
t.scores = (new**0.5)*1.0 / (n**0.5)
t.changed = False
return t.scores
"""
### Demo stuff
To run these at load time, add _@go_ (uncommented) on the line before.
Checks that we can find lost and distant things:
"""
@go
def _distances():
def closest(m,i,all):
return furthest(m,i,all,10**32,lambda x,y: x < y)
random.seed(1)
m = "any"
pop = [candidate(m) for _ in range(4)]
for i in pop:
j = closest(m,i,pop)
k = furthest(m,i,pop)
print "\n",\
gs(i.dec), g(scores(m,i)),"\n",\
gs(j.dec),"closest ", g(dist(m,i,j)),"\n",\
gs(k.dec),"furthest", g(dist(m,i,k))
print i
"""
A standard call to WHERE, pruning disabled:
"""
@go
def _where():
random.seed(1)
m, max, pop, kept = "model",100, [], Num()
for _ in range(max):
one = candidate(m)
kept + scores(m,one)
pop += [one]
slots = where0(verbose = True,
minSize = max**0.5,
prune = False,
wriggle = 0.3*kept.s())
n=0
for leaf in where(m, pop, slots):
n += len(leaf)
print n,slots
"""
Compares WHERE to GAC:
"""
@go
def _whereTiming():
def allPairs(data):
n = 8.0/3*(len(data)**2 - 1) #numevals WHERE vs GAC
for _ in range(int(n+0.5)):
d1 = any(data)
d2 = any(data)
dist("M",d1,d2)
random.seed(1)
for max in [32,64,128,256]:
m, pop, kept = "model",[], Num()
for _ in range(max):
one = candidate(m)
kept + scores(m,one)
pop += [one]
slots = where0(verbose = False,
minSize = 2, # emulate GAC
depthMax=1000000,
prune = False,
wriggle = 0.3*kept.s())
t1 = timing(lambda : where(m, pop, slots),10)
t2 = timing(lambda : allPairs(pop),10)
print max,t1,t2, int(100*t2/t1)



