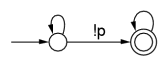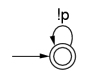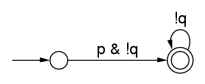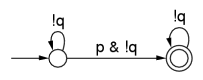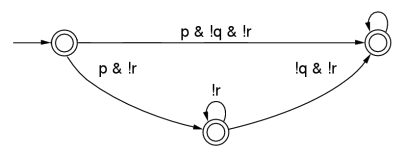
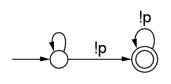
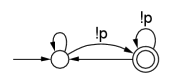
Büchi automata are used to represent temporal logic formulas. Büchi automata are different from normal finite-state machines: for normal finite-state machines, acceptance is defined as reaching an accept (or final) state. For Büchi automata, acceptance is defined as finding a cycle that includes an accept state; it must be possible to reach the accept state infinitely often.

As with the model checker SPIN, for example, Lurch uses Büchi automata representing the negation of the desired property. So for the examples on this page, the property given is violated by an execution in which the machine gets stuck in a cycle that includes an accept state. Note that Lurch, since it's an approximate search with a depth limit, can't tell for sure if we're really stuck in an accept cycle. So the "hash collisions" parameter is used as a sort of cycle-detection threshold: if we've seen the same global state n times, where n is the hash collision limit, it's assumed that we're stuck in that cycle and we'd see that state an infinite number of times if the search continued on to infinite depth (this is Lurch's very informal, randomized notion of fairness).

Lurch handles temporal logic properties the same way the model checker SPIN does. In fact the underlying program used to translate properties is "ltl2ba", which was written for SPIN. And the example properties on this page come from SPIN's online documentation (spinroot.com/spin/Doc/fm2003-spin-tutorial.pdf). To use ltl2ba with Lurch, download the source from spinroot.com/spin/Src/ltl2ba.tar.gz. (Note: I had to modify the ltl2ba files to compile them locally, so I've included the version that worked for me in the Lurch download.) Then compile ltl2ba and run the executable with the script ba2lu.awk, included with the Lurch download:

ltl2ba -d -f '[]p' | gawk -f 'ba2lu.awk'

The output is a little bit criptic. Here's what you get from the above command:

n: init. (p); -; init.
=init
#define p

Lines beginning with n: are the Büchi automaton, which is to be copied directly into the input model. If the Büchi automaton ends with =init, this means the initial state needs to be an accept state, so an equals sign should be added to every init in the Büchi automaton. Finally, any #define lines needed to be filled out with macro definitions and copied to the beginning of the input model.

[]p

"always p"

n: init. (1); -; init.
n: init. (!p); -; =accept_0.
n: =accept_0. (1); -; =accept_0.

For these automata, if it's possible to get to an accept cycle, the property's violated, so while they are nondeterministic and include the lambda transition, in effect the transition toward the accept state is preferred. Here, if we ever see !p, we go to the accept state, and since it's got a lambda transition back to itself, we're automatically in an accept cycle (note: if the machine blocks, i.e., it gets into a state from which no transition is enabled, it is reset back to its initial state; this is to imitate the behavior of a never clause, SPIN's representation of a Büchi automaton).

<>p

"eventually p"

n: =init. (!p); -; =init.

We go immediately to an accept state, but we must keep seeing !p forever to stay in the accept cycle.

p -> <>q

"p implies eventually q"

n: =init. (p & !q); -; =accept_2.
n: =accept_2. (!q); -; =accept_2.

From the initial state, if we ever see p but not q, we go to an accept state, at this point in the same situation as with "guarantee" above. So this is how implication works: at whatever point the left side is satisfied, we start there and try to satisfy the right side.

p -> (q U r)

"p implies q until r"

n: =init. (p & !r); -; =accept_2.
n: =init. (p & !r & !q); -; =accept_0.
n: =accept_2. (!r); -; =accept_2.
n: =accept_2. (!r & !q); -; =accept_0.
n: =accept_0. (1); -; =accept_0.

What executions are ok? First, if we never see p, the property is vacuously true; second, if we see p and r but not necessarily q; third, if we see p and q, continue to see q, and then at some point see r. What executions are not allowed? Any in which we see p but never r afterward, and any in which q is not continuously true from the time p is seen to the time r is seen. Note: this is "strong until" because the property is violated if we never see r; if we used "weak until" it would be ok if q continued forever. Although the syntax used by Lurch (really, the syntax used by ltl2ba underneath) doesn't include a weak until operator, it is possible to use []q | (q U r), which is equivalent to weak until.

(LTL2Buchi, an alternative to ltl2ba that includes the weak until operator, is available with NASA Ames' Java Pathfinder at javapathfinder.sourceforge.net.)

[]<>p

"always eventually p"

n: init. (1); -; init.
n: init. (!p); -; =accept_2.
n: =accept_2. (!p); -; =accept_2.

This property could also be called "progress". The idea is, from any point in execution, we want to make sure that we will still see p some time in the future. There should be no point from which we are no longer guaranteed to see p in the future.

<>[]p

"eventually always p"

n: init. (!p); -; =accept_1.
n: init. (1); -; init.
n: =accept_1. (!p); -; =accept_1.
n: =accept_1. (1); -; init.

Benjamin Franklin wrote: "...everything appears to promise that it will last; but in this world nothing is certain but death and taxes." Taxes are certain in the sense of the previous property, recurrence. Death is certain in the sense of this property, stability: all executions (no pun intended) lead to a point at which p remains true forever.

<>p -> <>q

"eventually p implies eventually q"

n: init. (!q); -; init.
n: init. (p & !q); -; =accept_2.
n: =accept_2. (!q); -; =accept_2.

If we ever see p, we will see q sometime after that. Note that the implication doesn't work the other way. It's possible to read the property as: if I know that p is coming some time in the future, then I need to make sure q also is coming some time in the future, but it doesn't matter which is first... Here is does matter, p has to come first, because of what we said about implication above.