Uncertainty, Fuzzy Logic

Reasoning and Uncertainty

The words figure and fictitious both derive from the same Latin root, fingere (to form, create). Beware! --M.J. Moroney

Everything is vague to a degree you do not realize :till you have tried to make it precise. --Bertrand Russell

I'm pretty certain that I need better ways to handle uncertainty. Many expressions of human knowledge are not crisp ideas. Rather, they are hedges, shades of gray.

Consider four problems in programming a game:

• Threat assessment: How many battalions to deploy when you don't have total knowledge of the enemies movements?
• Control: when chasing a target, you want to see some fluid gradual changes in tactics. Abrupt straight-line movements that suddenly change course would appear unnatural.
• Classification: how to combine information to yield hedge information like wimpy, easy, moderate, tough, formidable? How to combine these hedged classifications with other hedges to infer further information?
• How to do all the above that introduces some measure of unpredictability into the game?

The problem is that conventional principles of logic are very unfriendly towards uncertainty. In classical logic, things are either true or false. You do, you don't. Worse, if a model contains a single inconsistency, the whole theory is false. So one little doubt, one little "this or not this" and you are screwed. Not very helpful for introducing gradual degrees of hedged knowledge that may be contradictory.

This is not just a game playing problem. The drawbacks of classical logic are well known. Theoreticians like Lofti Zadeh offer a Principle of Incompatibility :

• "As the complexity of a system increases, our ability to make precise and yet significant statements about its behavior diminishes until a threshold is reached beyond which precision and significance (or relevance) become almost mutually exclusive characteristics."

• "It is in this sense that precise quantitative analyzes of the behavior of humanistic systems are not likely to have much relevance to the real worlds societal, political, economic and other types of problems which involve humans either as individuals or in groups."

Philosophers like Karl Popper claim that accessing 100% evidence on any topic a fool's goal. All "proofs" must terminate on premises; i.e. some proposition that we accept as true without testing, but which may indeed be wrong. In terms of most human knowledge, a recursion to base premises is fundamentally impractical. For example:

• Consider one individual trying to reproduce all the experiments that lead to our current understanding of atomic physics.
• Such an undertaking could longer than a lifetime and would be beyond the resources of most individuals (e.g. building a five kilometer long linear accelerator).
• Such a task has to be divided up and, sooner or later, our single researcher would have to accept on faith the validity of another researcher's statement that "while you were busy elsewhere, I did this, and I saw that. Trust me.".

There is much evidence for Popper's thesis. Gathering all the information required to remove all uncertainties can be very difficult:

• In the first study that isolated the thyroptin-releasing hormone (used in the brain), 300,000 sheep brains had to be filtered. This yielded 1.0 milligrams of purified hormone.
• The premise of the cs572 project is that we can't collect the information required to tune 28 variables in a software process model. I am continually surprised that this is the case. All software development organizations collect information but just try to access consistent samples of it!
• The (in)famous "Limits to Growth" study attempted to predict the international effects of continued global economic growth. Less than 0.1% of the data required for the models was available
• If the planet is too big, when is small small enough? In a complex system of only a modest number of variables and interconnections, any attempt to describe the system completely and measure the magnitude of all the links would be the work of many people over a lifetime

Experience with mathematical simulation suggest that an over-enthusiasm for quantitative analysis can confuse, rather than clarify, a domain. For systems whose parts are not listed in a catalog, which evolve together, which are difficult to measure, and which show unexpected capacity to form new connections, the results of (quantitative) simulation techniques have been less than impressive:

• The masses of data required make the procedure very costly.
• The demand for qualitative precision often forces the exclusion of many variables (e.g. stress in diabetes: poorly quantified but vitally important);
• the predictions apply only to the original single system from which the models were derived, and are not easily extended even to similar systems ([207], p4).

Anyway, why seek total knowledge? Some levels of uncertainty are a good thing:

• In a game simulation, you want some higglety pigglety . It would look unnatural if all leaves on all the trees all blow this way then that like soldiers on parade.
• When co-ordinating multiple agents, it is good to leave some room for local improvisation. Consider the phrase "close enough for jazz":
   
  While "close enough for jazz" sounds disparaging, it really isn't, in my view. The nature of jazz is to improvise on the basis of a known musical core, whether it's a melody or a set of harmonies. If it is TOO close to the original melody or other musical archetype, or too close for too long, it is no longer jazz, it's the original. "Close enough," it seems to me, would be close enough to recognize the musical skeleton behind what's being played, but not so close as to hamper the improvised self-expression at the heart of jazz.
  From SS.

Sometimes we can learn more by allowing some uncertainties. Creative solutions and insights can sometimes be found in a loosely constrained space than may be impossible in tightly constrained, certain spaces. For example,

• Enabling random search is a very useful tool. We have seen before that stochastic theorem provers have very nice generality properties.
• If we over fit our solutions to old data then our solutions may be brittle if any part of that old data changes. That is, even if total knowledge is available for a system, it can be useful to mutate that knowledge to see how changes to the background knowledge effect the outcome.
  • The premise of the NOVA project is that we don't want one solution. Rather, we want to find actions that are stable across the space of all possible solutions
  • In diagnosis, we may not want to explore scenarios that are exactly like prior knowledge of normal behavior. Rather, we want to explore abnormal deviations from normal. Also, in diagnosis, you can't reflect over multiple options unless your models can generate multiple options. That is, for diagnosis, you want models that can handle "don't know, it could be this or that".

• Q: do we call out the marines?
• A: depends on the size and proximity of the invading forces

             PROXIMITY
  SIZE       close   medium  far
  --------   ----------------------
  tiny       medium  low     low
  small      high    low     low
  moderate   high    medium  low
  large      high    high    medium
  

• (But how do we give meaning to all these symbols?.... see below.)

So we need to change classical logic. Uncertainty is unavoidable. Despite this, we persist and continue building systems of increasing size and internal complexity. Somehow, despite uncertainty, we can handle uncertainty and doubt and predict the future a useful percent of the time. How do we do it? How can we teach AI algorithms to do it?

Fuzzy Logic

Officially, there are rules. Unofficially, there are shades of gray. Fuzzy logic is one way to handle such shades of gray.

For example, consider the rule ``if not raining then play golf''. Strange to say, sometimes people play golf even in the rain. Sure, they may not play in a hurricane but a few drops of rain rarely stops the dedicated golfer.

Fuzzy logic tries to capture these shades of gray. Our golf rule means that we rush to play golf in the sunshine, stay home during hurricanes, and in between we may or may not play golf depending on how hard it is raining.

Fuzzy logic uses fuzzy sets. Crisp sets have sharp distinctions between true and falsehood (e.g. it is either raining or not). Fuzzy sets have blurred boundaries (e.g. it is barely raining). Typically, a membership function is used to denote our belief in some concept. For example, here are some membership functions for the belief that a number is positive. All these beliefs have the same membership function:

 1/(1+exp(-1*x*crisp))

Or, in another form...

(defun crisp (x a b crisp)
  "Return a point in a sigmoid function centered at (a - b)/2"
  (labels ((as100 (x min max)
	     (+ -50 (* 100 (/ (- x min) (- max min))))))
    (/ 1 (+ 1 (exp (* -1 (as100 x a b) crisp))))))

(defun fuzzy-grade (x &optional (a 0) (b 1) (slope 0.1))
  (crisp x a b slope))

where the crisp parameter controls how sharp is the boundary in our beliefs:

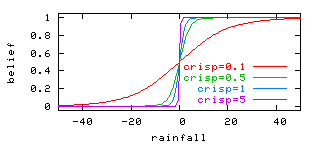
Note that for large crisp values the boundary looks like classical logic: at zero a number zaps from positive to negative. However, in the case of our golfing rule, there are shades of gray in between sunshine and hurricanes. We might believe in playing golf, even when there is a little rain around. For these situations, our beliefs are hardly crisp, as modeled by setting crisp to some value less than (say) one.

The crisp value lets us operationalize a set of linguistic variables or hedges such as ``barely'', ``very'', ``more or less'', ``somewhat,'' ``rather,'' ``sort of,'' and so on. In this approach, analysts debrief their local experts on the relative strengths of these hedges then add hedge qualifiers to every rule. Internally, this just means mapping hedges to crisp values. For example:

  definitely: crisp=10
  sort of:    crisp=0.5
  etc

Alternatively, analysts can ask the local experts to draw membership functions showing how the degrees of belief in some concept changes over its range. For example:

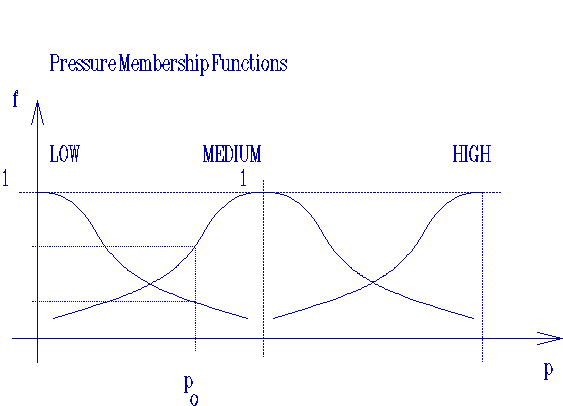
Sometimes, these can be mapped to mathematical functions as in the following:

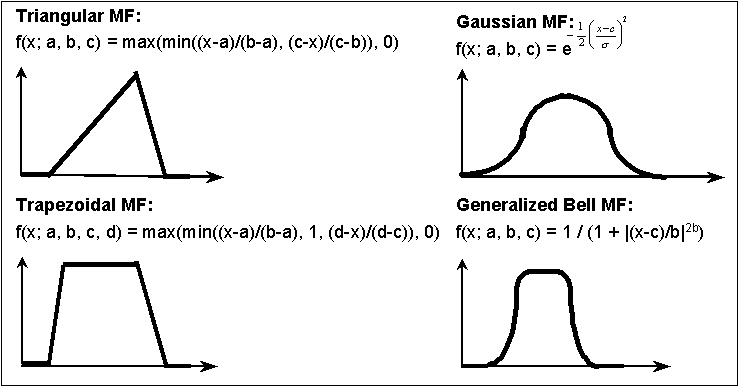
(defun fuzzy-triangle (x a b c) 
  (max 0 (min (/ (- x a) (- b a))
	      (/ (- c x) (- c b)))))

(defun fuzzy-trapezoid (x a b c d)
  (max 0 (min (/ (- x a) (- b a))
	      1
	      (/ (- d x) (- d c)))))

Note that the function need not be represented mathematically. If the local experts draw any shape at all, we could read off values from that drawing and store them in an array. For example, an analyst can construct an array of values for various terms, either as vectors or matrices. Each term and hedge can be represented as (say) a 7-element vector or 7x7 matrix. Each element of every vector and matrix a value between 0.0 and 1.0, inclusive, in what might be considered intuitively a consistent manner. For example, the term ``high'' could be assigned the vector

     0.0 0.0 0.1 0.3 0.7 1.0 1.0

and ``low'' could be set equal to the reverse of ``high,'' or

     1.0 1.0 0.7 0.3 0.1 0.0 0.0

Zadeh Operators

The AND, OR, NOT operators of boolean logic exist in fuzzy logic, usually defined as the minimum, maximum, and complement; i.e.

    [1]  truth (not A)   = 1.0 - truth (A)
    [2]  truth (A and B) = minimum (truth(A), truth(B))
    [3]  truth (A or B)  = maximum (truth(A), truth(B))

Or, in another form...

(defmacro $and (&rest l) `(min ,@l))
(defmacro $or  (&rest l) `(max ,@l))
(defun    $not (x)       (- 1 x))

When they are defined this way, the are called the Zadeh operators, because they were originally defined as such in Zadeh's original papers.

Here are some examples of the Zadeh operators in action:

 [1] truth (not A)   = 1.0 - truth (A)

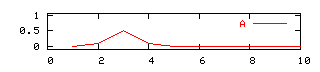
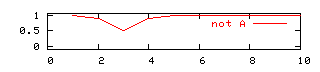
 [2] truth (A and B) = minimum (truth(A), truth(B))

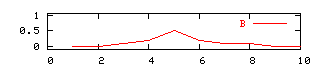
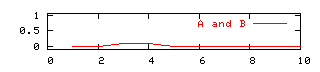
 [3]  truth (A or B)  = maximum (truth(A), truth(B))

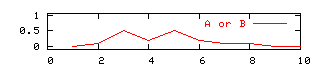
Here are some more examples:

Here's yet another example

Some researchers in fuzzy logic have explored the use of other interpretations of the AND and OR operations, but the definition for the NOT operation seems to be safe.

Note that if you plug just the values zero and one into the definitions [1],[2],[3], you get the same truth tables as you would expect from conventional Boolean logic. This is known as the EXTENSION PRINCIPLE, which states that:

The classical results of Boolean logic are recovered from fuzzy logic operations when all fuzzy membership grades are restricted to the traditional set {0, 1}.

Example 1

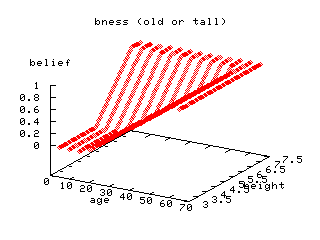
Assume that we have some fuzzy sub membership functions for combination of TALL and OLD things defined as follows:

 function tall(height) {
  if (height < 5 ) return Zero;
  if (height <=7 ) return (height-5)/2;
  return 1;
 }

 function old(age) {
   if (age <  18) return Zero;
   if (age <= 60) return (age-18)/42;
   return 1;
 }

 function a(age,height)   { return FAND(tall(height),old(age)) }
 function b(age,height)   { return FOR(tall(height), old(age)) }
 function c(height)       { return FNOT(tall(height)) }
 function abc(age,height) { 
        return FOR(a(age,height),b(age,height),c(height)) }

(The functions FNOR, FAND, FOR are the Zadeh operators.)

For compactness, we'll call our combination functions:

    a = X is TALL and X is OLD
    b = X is TALL or X is OLD
    c = not (X is TALL)
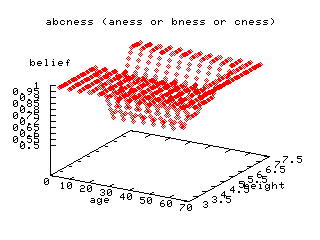
    abc= a or b or c

Here's the OLDness functions:

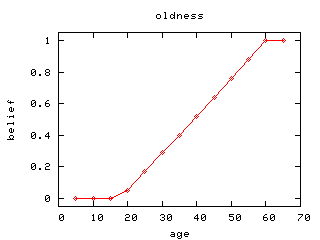
Here's the TALLness function:

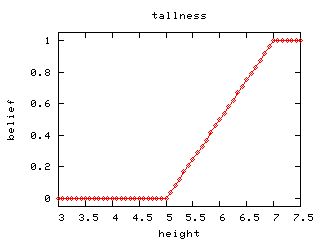
Here's (c); i.e. the not TALLness function:

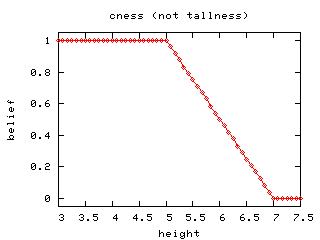
Here's (a): TALL and OLD

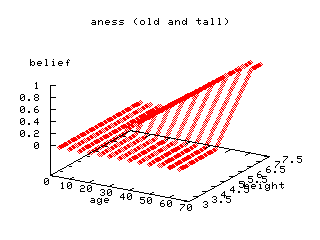
Here's (b): TALL or OLD

Here's (abc): a or b or c

In practice

Methodology, a fuzzy logic session looks like this:

Fuzzification:

Using membership functions, describe a situation.

Rule evaluation:

Apply fuzzy rules (e.g. using the Zadeh operators)

Defuzzification:

Obtaining the crisp or actual results:

• Apply some threshold to declare than any fuzzy belief over (e.g.) 0.2 is true and all others are false.
• Translate the resulting beliefs back through the membership functions to get a linguistic summary of the conclusion; e.g. happy is sort of true.
• Return the centroid of the computed membership function. This process can be very complex (using full integrals) or, as the following example shows, very simple.

  Suppose we have an output fuzzy set AMOUNT which has three members: ZERO, MEDIUM, and HIGH. We assign to each of these fuzzy set members a corresponding output value, say 0 for Zero, 40 for MEDIUM, and 100 for HIGH. A Defuzzification procedure might then be:

   return (ZERO*0 + MEDIUM*40 + HIGH*100)/(0+40+100)

Example 2: Do we Call out the Marines?

How close is the enemy?

• Close, medium, far?

How large is the enemy's forces?

• Tiny, small, moderate, large?

What is the size of the threat?

           PROXIMITY
SIZE       close   medium  far
--------   ----------------------
tiny       medium  low     low
small      high    low     low
moderate   high    medium  low
large      high    high    medium

We need some membership functions:

(defun dist (d what)  
  (case what
    (range    '(close medium far))
    (close     (fuzzy-triangle   d -30 0 30))
    (medium    (fuzzy-trapezoid  d 10 30  50 70))
    (far       (fuzzy-grade      d 0.3  50 100))
    (t         (warn "~a not known to dist" what))))

(defun size (s what)
  (case what
    (range    '(tiny small moderate large))
    (tiny      (fuzzy-triangle  s -10 0 10))
    (small     (fuzzy-trapezoid s 2.5 10 15 20))
    (moderate  (fuzzy-trapezoid s 15 20 25 30))
    (large     (fuzzy-grade     s 0.3 25 40))
    (t         (warn "~a not known to size " what))))

And we'll need to model the above table:

(defun fuzzy-deploy (d s what)
  (macrolet (($if (x y) `($and (dist d ',x) (size s ',y))))
    (case what
      (range    '(low medum high))
      (low       ($or ($if medium tiny)
		      ($if far    tiny)
		      ($if medium small)
		      ($if far    small)))
      (medium    ($or ($if close  tiny)
		      ($if medium moderate)))
      (high      ($or ($if close  small)
		      ($if close  moderate)
		      ($if close  large)
		      ($if medium moderate)))
      (t         (warn "~a not known to fuzzy-deploy" what)))))

Finally, we need a defuzzication function:

(defun defuzzy-deploy (&key distance size)
  "Return how many marines to deploy?"
  (let ((low    (fuzzy-deploy distance size 'low   ))
	(medium (fuzzy-deploy distance size 'medium))
	(high   (fuzzy-deploy distance size 'high  )))
    (round 
     (/ (+ (* 10 low) (* 30 medium) (* 50 high))
	(+ low medium high)))))

So, how many marines to deploy?

(defuzzy-deploy :distance 25 :size 8)) ==> 19