Prolog is the Fortran of logic programming: it was the first of its kind, it was much criticised, and it is still widely used.
George Santayana: "Those who do not remember the past are condemned to repeat it."
Tim Menzies: "Those who do not study Prolog are condemned to repeat it."
PROLOG came from natural langauge research in the 1970s, 1980s and was an attempt to treat human texts as logic formulae. Hence, before we can explain NL in PROLOG, we must explain PROLOG.
Functions map inputs to outputs.
Predicates define constraints on variables.
Functions run.
Predictes match.
Functions return some output.
Predicates only return yes or no. If "yes", then as a side effect, they may add bindings to variables.
(Adapted from Robert F. Rossa: rossa@csm.astate.edu).
We show below a Prolog program consisting entirely of simple clauses or facts. This set of facts is a database about a family.
/* family.pl - a simple database for a family */ gender(al,male). gender(anne,female). gender(arthur,male). gender(amber,female). gender(boris,male). gender(barbara,female). gender(betty,female). gender(buck,male). gender(carla,female). gender(charles,male). gender(cora,female). gender(cuthbert,male). gender(cecilia,female). gender(calvin,male). father(arthur,buck). father(al,buck). father(amber,buck). father(anne,boris). father(barbara,charles). father(betty,cuthbert). father(boris,charles). father(buck,calvin). mother(al,barbara). mother(anne,betty). mother(arthur,barbara). mother(amber,barbara). mother(boris,carla). mother(barbara,carla). mother(betty,cora). mother(buck,cecilia).
We can load this database into a Prolog interpreter.
swipl -f family.pl ?-
Now the interpreter is waiting for us to query it. Every query must end with a period. When we query the interpreter, it will give us the first answer it finds, based on the facts in the database. If we want more answers, we enter a semicolon. If we don't want any more answers to that query, we just enter a carriage return. Thus consider the sequence that follows.
?- father(X,Y). X=arthur, Y=buck; X=al, Y=buck; X=amber, Y=buck; X=anne, Y=boris; X=barbara, Y=charles; X=betty, Y=cuthbert; X=boris, Y=charles; X=buck, Y=calvin no ?-
So the Father successed many times, and as a side-effect, printed some bindings. Then it automatically backtracked (on the ";" command) to find other bindings.
In this example, PROLOG answers "no" since no data satisfies the following constraints.
?- mother(al,betty). no ?- mother(al,barbara). yes ?-We can build more complex queries like the following, to find a grandmother of al.
?- mother(al,X),mother(X,Y). X=barbara, Y=carla yes ?-
Which is to say that we are looking for a pattern and where "X" and "Y" satisfy some constraints.
BTW, identifiers that start with an upper case letter are variables, and those that start with lower case letters are constants.
parent(X,Y) :- father(X,Y). parent(X,Y) :- mother(X,Y).The symbol ':-' should be read as "if". Now we can query as follows.
?- parent(al,Y). Y=buck; Y=barbara yes ?-We can now build a rule that uses the parent rules.
grandfather(X,Y) :- parent(X,Z),father(Z,Y).and ask questions like
?- grandfather(anne,Y). Y=charles; Y=cuthbert; no ?-
Note that PROLOG has no pre-defined input output variables- everything is a constraint. So we could have equally posed the above query as:
?- grandfather(X,anne). X=anne; no ?-
The scope of variables is one clause; there is no such thing as a global variable.
When Prolog tries to answer a query, it goes through a matching process. It tries to match the predicates on the right-hand side of the rule from left to right, binding variables when it finds a match. If a match fails, it may be because of the bondings in matches to the left. In that case, the interpreter backtracks - it returns to the nearest previous binding and tries to find a different match. If that fails, it backtracks some more.
We can make Prolog print out all the answers to a question by deliberately making it fail, using the fail predicate.
?- grandfather(X,Y),write('X='),write(X),write(', Y='),write(Y),nl,fail.
X=arthur, Y=calvin
X=al, Y=calvin
X=amber, Y=calvin
X=anne, Y=charles
X=al, Y=charles
X=anne, Y=cuthbert
X=arthur, Y=charles
X=amber, Y=charles
no
?-
Prolog lists have heads and tails (think "car" and "cdr").
member(A, [A|_]).
member(A, [_|B]) :-
member(A, B).
So, of course,...
?- member(a,[c,b,a]). true
But Prolog can bactrack to find all repeated members of a list:
?- member(a,[c,a,b,a]). true ; true
Also, we can find all members of a list:
?- member(X,[a,b,c]). X = a; X = b; X = c
Also, Prolog is a relational language. Variables are not inputs and outputs but concepts woven together by constraints. Also, we only need to partially specify the I/O to query those constraints:
?- member(name=What, [age=20,shoesize=12,name=tim]). What = tim .
(If this is causing stress, just chant to yourself: in Prolog, we don't code; rather, we draw the shape of the solution.)
This can get really funky. Here's the standard definition of how to append two lists:
append([], A, A).
append([A|B], C, [A|D]) :-
append(B, C, D).
Which works in the expected way:
?- append([a,b,c],[d,e,f],Out). Out = [a, b, c, d, e, f].
But any of these arguments can be left unspecified to achieve neat results:
; find the third thing in a list ?- append([ _, _, Third], _, [alice,john,mike,tim,veronica,wendy]). Third = mike ; find the list before "tim" ?- append(Before, [tim | _], [alice,john,mike,tim,veronica,wendy]). Before = [alice, john, mike] ; find the list after "tim" ?- append(_, [tim | After], [alice,john,mike,tim,veronica,wendy]). After = [veronica, wendy]
You can even write "member" using "append":
member1(X,L) :- append(_,[X|_],L). ?- member1(a,[b,c,a]). true . ?- member1(X,[b,c,a]). X = b ; X = c ; X = a ; fail.
Now with great power comes great responsbility. If you ask find all lists which can contain 'a', you can get an infinite set (of course).
?- member(a,L). L = [ a |_G246] ; L = [_G245, a |_G249] ; L = [_G245, _G248, a |_G252] ; L = [_G245, _G248, _G251, a |_G255] ; L = [_G245, _G248, _G251, _G254, a |_G258] ; L = [_G245, _G248, _G251, _G254, _G257, a |_G261] ; L = [_G245, _G248, _G251, _G254, _G257, _G260, a |_G264] ; L = [_G245, _G248, _G251, _G254, _G257, _G260, _G263, a |_G267] ;
Lesson: logic, like anything else, must be used wisely.
(Written by yours truly.)
Prolog variables support generalizations. For example, the following monkeys and bananas solution supports climbing onto a box anywhere in the room as well as push anything to anywhere.
It uses the following database:
% making Move in State1 results in State2; % move( State1, Move, State2) % representing the current state % state( MonkeyHorizontal, MonkeyVertical, BoxPosition, HasBanana)
Our goal is to get the banana.
goal(state(_,_,_,has)).
Our start state...
start(state(atfloor,onfloor,atwindow,hasnot)).
This is how we can get from state1 to state2:
canget( S,[]) :- goal(S). % base case canget( State1,[Act|Rest]) :- % general case move( State1, Act, State2), % Do something canget( State2,Rest). % Repeat
The knowledge base:
move( state( middle, onbox, middle, hasnot), % Before move
grasp, % Grasp banana
state( middle, onbox, middle, has) ). % After move
move( state( P, onfloor, P, H),
climb, % Climb box
state( P, onbox, P, H) ).
move( state( P1, onfloor, P1, H),
push( P1, P2), % Push box from P1 to P2
state( P2, onfloor, P2, H) ).
move( state( P1, onfloor, B, H),
walk( P1, P2), % Walk from P1 to P2
state( P2, onfloor, B, H) ).
Main program:
main :- start(S0), canget(S0, Steps),
forall(member(Step,Steps), (print(Step),nl)).
Output:
?- main. walk(atfloor, atwindow) push(atwindow, middle) climb grasp true ;
We pause here (even though we asked PROLOG to backtrack and find more solutions with the ";" command) to comment that we we got to the bananas.
Moving on, as we backtrack, we see that the solution gets longer. This is not a bug. What is going on?
walk(atfloor, atwindow) push(atwindow, _G251) push(_G251, middle) climb grasp true ; % new solution found walk(atfloor, atwindow) push(atwindow, _G251) push(_G251, _G262) push(_G262, middle) climb grasp true ; % another solution found walk(atfloor, atwindow) push(atwindow, _G251) push(_G251, _G262) push(_G262, _G273) push(_G273, middle) climb grasp true . % yet another solution found
Hmm.... looks like we need to control how far the money walks.
(Adapted from John Fisher's excellent Prolog tutorial.)
Prolog's hardwired search is depth-first through its list of clauses. But this can easily be changed. For example, in this section we will code up DFID in Prolog.
For our first DFID, we control the size of the list that shows the steps taken to reach the goal. We can build that leash using the following trick:
?- between(1,5,N), length(List, N). N = 1, List = [_G292] ; N = 2, List = [_G292, _G295] ; N = 3, List = [_G292, _G295, _G298] ; N = 4, List = [_G292, _G295, _G298, _G301] ; N = 5, List = [_G292, _G295, _G298, _G301, _G304].
We will use this trick to define dfid as a loop around the monkey's "canget" predicate:
dfid(Max) :-
start(S0),
between(1,Max,Depth), % on backtracking, Depth=1,2,3,...
length(Steps,Depth), % Steps is a list of size Depth
print(leash(Steps)),nl,
canget(S0,Steps),
print(Depth),nl,
forall(member(Step,Steps), (tab(4),print(Step),nl)).
For example:
?- dfid(5), fail. % backtrack through all solutions.
leash([_G254])
leash([_G254, _G257])
leash([_G254, _G257, _G260])
leash([_G254, _G257, _G260, _G263])
4
walk(atfloor, atwindow)
push(atwindow, middle)
climb
grasp
leash([_G254, _G257, _G260, _G263, _G266])
5
walk(atfloor, atwindow)
push(atwindow, _G280)
push(_G280, middle)
climb
grasp
5
walk(atfloor, atwindow)
push(atwindow, middle)
walk(middle, middle)
climb
grasp
5
walk(atfloor, _G272)
walk(_G272, atwindow)
push(atwindow, middle)
climb
grasp
Prolog has a shorthand for writing grammar rules:
sentence --> nominal_phrase, verbal_phrase. verbal_phrase --> modlist,verb. nominal_phrase --> article, noun. article --> [the]. noun --> [dog]. verb --> [runs]. verb --> [barks]. modlist --> []. modlist --> [sadly], modlist.
(Note that modlist is zero or more "sadly"s.).
If we load this into PROLOG, we get
swipl -f english.pl ?- listing(sentence). sentence(A, C) :- nominal_phrase(A, B), verbal_phrase(B, C). true. ?- listing(verb). verb([runs|A], A). verb([barks|A], A). true. ?-
That is, PROLOG interprets grammars as rules. Terminals (like runs) are assumed to be members of a list.
We can ask PROLOG now, what sentences are valid in this grammar:
?- sentence(X,[]). X = [the, dog, runs] ; X = [the, dog, barks]; no ?-
We can also ask, is a sentence valid:
?- sentence([the,dog,runs],X). X = [] . ?- sentence([the,dog,sadly,sadly,sadly,runs],X). X = [] . ?- sentence([the,dog,flies],X). false. ?-
What is wrong with this grammar?
s --> np, vp. np --> det, n. np --> pro. vp --> v, np. vp --> v. det --> [the]. det --> [a]. n --> [woman]. n --> [man]. v --> [shoots]. pro --> [he]. pro --> [she]. pro --> [him]. pro --> [her].
Seems to work ok...
?- s([she,shoots,him],[ ]). yes ?- s([a,woman,shoots,him],[ ]). yes
But these sentences are odd...
?- s([a,woman,shoots,he],[ ]). yes ?- s([her,shoots,a,man],[ ]). yes s([her,shoots,she],[ ]). yes
The DCG ignores some basic facts about English
It is obvious what we need to do:
How do we do this? Version 1 (verbose, naive):
s --> np_subject, vp. np_subject --> det, n. np_object --> det, n. np_subject --> pro_subject. np_object --> pro_object. vp --> v, np_object. vp --> v. det --> [the]. det --> [a]. n --> [woman]. n --> [man]. v --> [shoots]. pro_subject --> [he]. pro_subject --> [she]. pro_object --> [him]. pro_object --> [her].
Nice way using extra arguments:
s --> np(subject), vp. np(_) --> det, n. np(X) --> pro(X). vp --> v, np(object). vp --> v. det --> [the]. det --> [a]. n --> [woman]. n --> [man]. v --> [shoots]. pro(subject) --> [he]. pro(subject) --> [she]. pro(object) --> [him]. pro(object) --> [her].
Better:
?- s([she,shoots,him],[ ]). yes ?- s([she,shoots,he],[ ]). no ?-
What is really going on? Recall that the rule:
s --> np,vp.is really syntactic sugar for:
s(A,B):- np(A,C), vp(C,B).The rule
s --> np(subject),vp.translates into:
s(A,B):- np(subject,A,C), vp(C,B).so, in effect, we have added a guard to the computation.

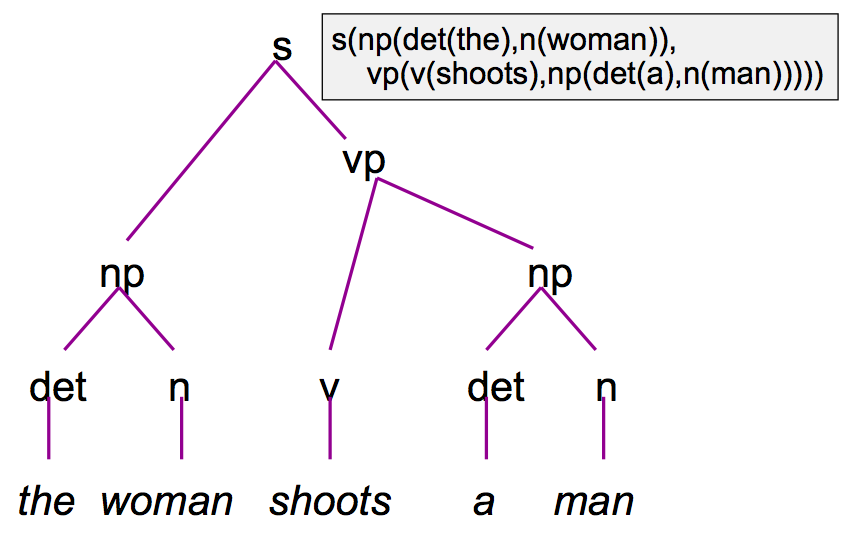
DCG that builds parse tree
s(s(NP,VP)) --> np(subject,NP), vp(VP np(_,np(Det,N)) --> det(Det), n(N). np(X,np(Pro)) --> pro(X,Pro). vp(vp(V,NP)) --> v(V), np(object,NP). vp(vp(V)) --> v(V)). det(det(the)) --> [the]. det(det(a)) --> [a]. n(n(woman)) --> [woman]. n(n(man)) --> [man]. v(v(shoots)) --> [shoots]. pro(subject,pro(he)) --> [he]. pro(subject,pro(she)) --> [she]. pro(object,pro(him)) --> [him]. pro(object,pro(her)) --> [her].
?- s(T,[he,shoots],[]). T = s(np(pro(he)),vp(v(shoots))) yes
It turns out that tree-traversal and computation are closely linked. E.g. descending into a tree based on a certain symbol is the same a conditional block with a guard.
PROLOG adds a {X} construct to its grammar rules that let you do primitive computations.
number(0) --> [zero].
number(N) --> digit(H), [hundred],
and_tens(T), {N is H * 100 + T}.
number(N) --> sub_tens(N).
and_tens(0) --> [].
and_tens(N) --> [and], sub_tens(N).
sub_tens(N) --> digit(N).
sub_tens(N) --> teen(N).
sub_tens(N) --> tens(T), and_digit(D), {N is T + D}.
and_digit(0) --> [].
and_digit(N) --> digit(N).
digit(1) --> [one]. teen(10) --> [ten].
digit(2) --> [two]. teen(11) --> [eleven].
digit(3) --> [three]. teen(12) --> [twelve].
digit(4) --> [four]. teen(13) --> [thirteen].
digit(5) --> [five]. teen(14) --> [fourteen].
digit(6) --> [six]. teen(15) --> [fifteen].
digit(7) --> [seven]. teen(16) --> [sixteen].
digit(8) --> [eight]. teen(17) --> [seventeen].
digit(9) --> [nine]. teen(18) --> [eighteen].
teen(19) --> [nineteen].
tens(20) --> [twenty].
tens(30) --> [thirty].
tens(40) --> [forty].
tens(50) --> [fifty].
tens(60) --> [sixty].
tens(70) --> [seventy].
tens(80) --> [eighty].
tens(90) --> [ninety].
The associated program now responds to queries of the following type:
[user] ?- number(Value, [ two, hundred, and, twenty, three ], []). Value = 223 yes
Besides performing this syntactical analysis and calculating the value, the program is also capable of providing an appropriate verbal expression for a given value (synthesis).
[user] ?- number(101, X, []). X = [one,hundred,and,one]
Can a computer understand a human? Lets test that. Let human ask questions about a domain and see if the machine can understand those questions w.r.t. the background knowledge of that domain?
It turns out this is a three-part problem:
a, some, the[singular] exists(X,R & S) no not exists(X,R & S) every, all not exists(X,R & not S) the[plural] exists(X,setof(X,R,X) & S) one, two, ... numeral(N) numberof(X,R & S,N) which, what answer(X) <= R & S how many answer(N) <= numberof(X,R & S,N)
Some birds migrate.
exists(X,bird(X) & migrates(X)).
The population of Britain exceeds 50 million.
exists(X,population(britain,X) & X > 50000000).There are no rivers in Antarctica.
not exists(X,river(X) & in(X,antarctica)).Man inhabits every continent.
not exists(X,continent(X) & not inhabits(man,X)).Jupiter is the largest of the planets.
exists(X,setof(X,planet(X),X) & largest(X,jupiter)).The Rhine flows through three countries.
numberof(X,country(X) & flows through(rhine,X),3).Which birds migrate?
answer(X) <= bird(X) & migrates(X).
How many countries export oil?
answer(N) <= numberof(X,country(X) & exports(X,oil),N).
Which European country exports no arms to coun- tries in Africa?
answer(C) <= european(C) & country(C) &
not exists(X, arm(X) &
exists(C1, country(C1) & in(Cl,africa) &
exports(C,X,C1) ) )
"For any C, C is an answer if C is European and C is a country and it cannot be shown that there is some X such that X is an armament and there is some C1 such that C1 is a country and C1 is in Africa and C exports X to CI"
Move common tests out of inner loop. Peek at the size of each DB and match on smaller things before longer things.
answer(C) <= country(C) &
borders (C,mediterranean) &
exists(Cl,country(C1) & asian(C1) &
borders(C,C 1))
After planning, the logical form is transformed into:
answer(C) <= borders(C,mediterranean) &
{country(C)} & {borders(C,C1) &
{asian(C1) & {country(C1)}}}
Countries
... country(uruguay,south_america,-32,55,68548,2990000,montevideo,peso). country(venezuela,south_america,8,65,352143,11520000,caracas,bolivar). country(vietnam,southeast_east,17,-107,126436,41850000,hanoi,dong). country(west_germany,western_europe,52,-9,95815,61970000,bonn,deutsche_mark). country(western_samoa,australasia,-14,172,1133,150000,apia,tala). country(yemen,middle_east,15,-44,75289,1600000,sana,rial). country(yugoslavia,southern_europe,44,-20,98766,21126000,belgrade,dinar). country(zaire,central_africa,-3,-23,905063,23560000,kinshasa,zaire). country(zambia,southern_africa,-15,-28,290724,4640000,lusaka,kwacha). country(zimbabwe,southern_africa,-20,-30,150333,5690000,salisbury,rhodesian_dollar).Rivers:
... river(senegal_river,[atlantic,senegal,mali,guinea]). river(tagus,[atlantic,portugal,spain]). river(vistula,[baltic,poland]). river(volga,[black_sea,soviet_union]). river(volta,[atlantic,ghana,upper_volta]). river(yangtze,[pacific,china]). river(yenisei,[arctic_ocean,soviet_union,mongolia]). river(yukon,[pacific,united_states,canada]). river(zambesi,[indian_ocean,mozambique,zambia,angola]).World:
flows(R,C1,C2) :- river(R,L), links(L,C2,C1). first([X|_],X). last([X],X). last([_|L],X) :- last(L,X). links([X1,X2|_],X1,X2). links([_|L],X1,X2) :- links(L,X1,X2).Borders:
borders(persian_gulf,saudi_arabia). borders(persian_gulf,united_arab_emirates). borders(red_sea,israel). borders(red_sea,jordan). borders(red_sea,saudi_arabia). borders(red_sea,yemen). borders(red_sea,egypt). borders(red_sea,ethiopia). borders(red_sea,sudan).Contains
contains0(west_germany,hamburg). contains0(west_germany,rhine). contains0(yugoslavia,danube). contains0(zaire,congo_river). contains0(zambia,congo_river). contains0(zambia,zambesi).
Parse: 0.0168457sec.
whq
$VAR
1
s
np
3+plu
np_head
int_det(B)
[]
river
[]
verb(be,active,pres+fin,[],pos)
void
[]
Semantics: 0.0170898sec.
answer([B]) :-
river(B)
& exists B
true
Planning: 0.0sec.
answer([B]) :-
river(B)
& exists B
true
amazon, amu_darya, amur, brahmaputra, colorado, congo_river, cubango, danube, don, elbe, euphrates, ganges, hwang_ho, indus, irrawaddy, lena, limpopo, mackenzie, mekong, mississippi, murray, niger_river, nile, ob, oder, orange, orinoco, parana, rhine, rhone, rio_grande, salween, senegal_river, tagus, vistula, volga, volta, yangtze, yenisei, yukon and zambesi.
Reply: 0.166992sec.
what countries are there in europe ?
Parse: 0.0500488sec.
whq
$VAR
1
s
np
3+plu
np_head
int_det(B)
[]
country
[]
verb(be,active,pres+fin,[],pos)
void
pp
prep(in)
np
3+sin
name(europe)
[]
Semantics: 0.032959sec.
answer([B]) :-
country(B)
& in(B,europe)
Planning: 0.0sec.
answer([B]) :-
in(B,europe)
& {country(B)}
albania, andorra, austria, belgium, bulgaria, cyprus, czechoslovakia, denmark, east_germany, eire, finland, france, greece, hungary, iceland, italy, liechtenstein, luxembourg, malta, monaco, netherlands, norway, poland, portugal, romania, san_marino, spain, sweden, switzerland, united_kingdom, west_germany and yugoslavia.
Reply: 0.199951sec.
which is the largest african country ?
Parse: 0.0500488sec.
whq
$VAR
1
s
np
3+sin
wh(B)
[]
verb(be,active,pres+fin,[],pos)
arg
dir
np
3+sin
np_head
det(the(sin))
sup
most
adj
large
adj
african
country
[]
[]
Semantics: 0.0339356sec.
answer([B]) :-
exists C
C = setof D:E
country(E)
& area(E,D)
& african(E)
& aggregate(max,C,B)
Planning: 0.0500488sec.
answer([B]) :-
exists C
C = setof D:E
african(E)
& {country(E)}
& area(E,D)
& aggregate(max,C,B)
sudan.
Reply: 0.300049sec.
what is the ocean that borders african countries and that borders asian countries ?
Parse: 0.0827637sec.
whq
$VAR
1
s
np
3+sin
wh(B)
[]
verb(be,active,pres+fin,[],pos)
arg
dir
np
3+sin
np_head
det(the(sin))
[]
ocean
conj
and
rel
$VAR
2
s
np
3+sin
wh(C)
[]
verb(border,active,pres+fin,[],pos)
arg
dir
np
3+plu
np_head
generic
adj
african
country
[]
[]
rel
$VAR
3
s
np
3+sin
wh(D)
[]
verb(border,active,pres+fin,[],pos)
arg
dir
np
3+plu
np_head
generic
adj
asian
country
[]
[]
[]
Semantics: 0.100098sec.
answer([B]) :-
ocean(B)
& exists C
country(C)
& african(C)
& borders(B,C)
& exists D
country(D)
& asian(D)
& borders(B,D)
Planning: 0.0500488sec.
answer([B]) :-
exists C D
ocean(B)
& { borders(B,C)
& {african(C)}
& {country(C)} }
& { borders(B,D)
& {asian(D)}
& {country(D)} }
indian_ocean.
Reply: 0.25sec.
how many countries does the danube flow through ?
Parse: 0.065918sec.
whq
$VAR
1
s
np
3+sin
name(danube)
[]
verb(flow,active,pres+fin,[],pos)
[]
pp
prep(through)
np
3+plu
np_head
quant(same,wh(B))
[]
country
[]
Semantics: 0.0168457sec.
answer([B]) :-
B = numberof C
country(C)
& flows(danube,C)
Planning: 0.0158691sec.
answer([B]) :-
B = numberof C
flows(danube,C)
& {country(C)}
6.
Reply: 0.032959sec.
what is the total area of countries south of the equator and not in australasia ?
Parse: 0.0500488sec.
whq
$VAR
1
s
np
3+sin
wh(B)
[]
verb(be,active,pres+fin,[],pos)
arg
dir
np
3+sin
np_head
det(the(sin))
adj
total
area
pp
prep(of)
np
3+plu
np_head
generic
[]
country
conj
and
reduced_rel
$VAR
2
s
np
3+plu
wh(C)
[]
verb(be,active,pres+fin,[],pos)
arg
pred
pp
prep(southof)
np
3+sin
name(equator)
[]
[]
reduced_rel
$VAR
3
s
np
3+plu
wh(D)
[]
verb(be,active,pres+fin,[],neg)
arg
pred
pp
prep(in)
np
3+sin
name(australasia)
[]
[]
[]
Semantics: 0.132813sec.
answer([B]) :-
exists C
C = setof D:[E]
area(E,D)
& country(E)
& southof(E,equator)
& \+in(E,australasia)
& aggregate(total,C,B)
Planning: 0.0830078sec.
answer([B]) :-
exists C
C = setof D:[E]
southof(E,equator)
& area(E,D)
& {country(E)}
& {\+in(E,australasia)}
& aggregate(total,C,B)
10228 ksqmiles.
Reply: 0.25sec.
is there some ocean that does not border any country ?
Parse: 0.0500488sec.
q
s
there
verb(be,active,pres+fin,[],pos)
arg
dir
np
3+sin
np_head
det(some)
[]
ocean
rel
$VAR
1
s
np
3+sin
wh(B)
[]
verb(border,active,pres+fin,[],neg)
arg
dir
np
3+sin
np_head
det(any)
[]
country
[]
[]
[]
Semantics: 0.032959sec.
answer([]) :-
exists B
ocean(B)
& \+
exists C
country(C)
& borders(B,C)
Planning: 0.032959sec.
answer([]) :-
exists B
{ ocean(B)
& { \+
exists C
borders(B,C)
& {country(C)} } }
Yes.
Reply: 0.0158691sec.
what are the continents no country in which contains more than two cities whose population exceeds 1 million ?
Parse: 0.184082sec.
whq
$VAR
1
s
np
3+plu
wh(B)
[]
verb(be,active,pres+fin,[],pos)
arg
dir
np
3+plu
np_head
det(the(plu))
[]
continent
rel
$VAR
2
s
np
3+sin
np_head
det(no)
[]
country
pp
prep(in)
np
3+plu
wh(C)
[]
verb(contain,active,pres+fin,[],pos)
arg
dir
np
3+plu
np_head
quant(more,nb(2))
[]
city
rel
$VAR
3
s
np
3+sin
np_head
det(the(sin))
[]
population
pp
poss
np
3+plu
wh(D)
[]
verb(exceed,active,pres+fin,[],pos)
arg
dir
np
3+sin
np_head
quant(same,nb(1))
[]
million
[]
[]
[]
[]
Semantics: 0.0998535sec.
answer([B]) :-
B = setof C
continent(C)
& \+
exists D
country(D)
& in(D,C)
& exists E
E = numberof F
city(F)
& exists G
population(F,G)
& exceeds(G,1--million)
& in(F,D)
& E>2
Planning: 0.0500488sec.
answer([B]) :-
B = setof C
continent(C)
& \+
exists D
country(D)
& in(D,C)
& exists E
E = numberof F
city(F)
& exists G
population(F,G)
& exceeds(G,1--million)
& in(F,D)
& E>2
[africa,antarctica,australasia].
Reply: 25.0sec.
which country bordering the mediterranean borders a country that is bordered by a country whose population exceeds the population of india ?
Parse: 0.116943sec.
whq
$VAR
1
s
np
3+sin
np_head
int_det(B)
[]
country
reduced_rel
$VAR
2
s
np
3+sin
wh(C)
[]
verb(border,active,inf,[prog],pos)
arg
dir
np
3+sin
name(mediterranean)
[]
[]
verb(border,active,pres+fin,[],pos)
arg
dir
np
3+sin
np_head
det(a)
[]
country
rel
$VAR
3
s
np
3+sin
wh(D)
[]
verb(border,passive,pres+fin,[],pos)
[]
pp
prep(by)
np
3+sin
np_head
det(a)
[]
country
rel
$VAR
4
s
np
3+sin
np_head
det(the(sin))
[]
population
pp
poss
np
3+sin
wh(E)
[]
verb(exceed,active,pres+fin,[],pos)
arg
dir
np
3+sin
np_head
det(the(sin))
[]
population
pp
prep(of)
np
3+sin
name(india)
[]
[]
[]
Semantics: 0.116943sec.
answer([B]) :-
country(B)
& borders(B,mediterranean)
& exists C
country(C)
& exists D
country(D)
& exists E
population(D,E)
& exists F
population(india,F)
& exceeds(E,F)
& borders(D,C)
& borders(B,C)
Planning: 0.0830078sec.
answer([B]) :-
exists C D E F
population(india,F)
& borders(B,mediterranean)
& {country(B)}
& { borders(B,C)
& {country(C)}
& { borders(D,C)
& {country(D)}
& { population(D,E)
& {exceeds(E,F)} } } }
turkey.
Reply: 1.09985sec.
which countries have a population exceeding 10 million ?
Parse: 0.0500488sec.
whq
$VAR
1
s
np
3+plu
np_head
int_det(B)
[]
country
[]
verb(have,active,pres+fin,[],pos)
arg
dir
np
3+sin
np_head
det(a)
[]
population
reduced_rel
$VAR
2
s
np
3+sin
wh(C)
[]
verb(exceed,active,inf,[prog],pos)
arg
dir
np
3+plu
np_head
quant(same,nb(10))
[]
million
[]
[]
[]
Semantics: 0.0671387sec.
answer([B]) :-
country(B)
& exists C
exceeds(C,10--million)
& population(B,C)
Planning: 0.0158691sec.
answer([B]) :-
exists C
country(B)
& { population(B,C)
& {exceeds(C,10--million)} }
afghanistan, algeria, argentina, australia, bangladesh, brazil, burma, canada, china, colombia, czechoslovakia, east_germany, egypt, ethiopia, france, india, indonesia, iran, italy, japan, kenya, mexico, morocco, nepal, netherlands, nigeria, north_korea, pakistan, peru, philippines, poland, south_africa, south_korea, soviet_union, spain, sri_lanka, sudan, taiwan, tanzania, thailand, turkey, united_kingdom, united_states, venezuela, vietnam, west_germany, yugoslavia and zaire.
Reply: 0.466064sec.