These notes extend the excellent lecture notes of written for CS472, Fall 2007, by Thorsten Joachims, CS, Cornell.
Further Reading:
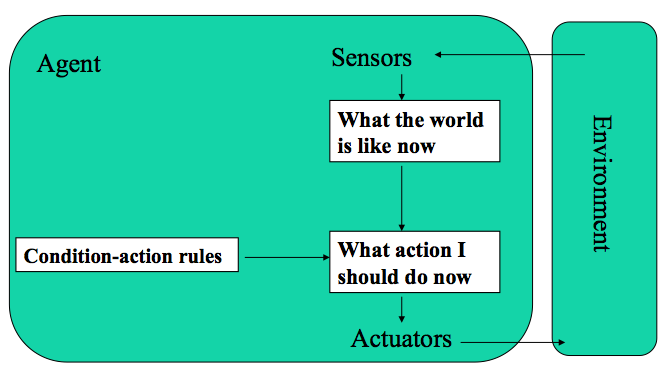
Agent: Anything that can be viewed as perceiving its environment through sensors and acting upon that environment through actuators.
Agent Function: Agent behavior is determined by the agent function that maps any given percept sequence to an action.
Agent Program: The agent function for an artificial agent will be implemented by an agent program.

Agent selects actions on the basis of the current percept - ignores history.
System will only work if the correct decision can be made on the basis of the current sensor input and if there are rules for all combinations of inputs.
Anything at all complicated will require that the system maintain an internal state, e.g. previous three sensor snapshots.
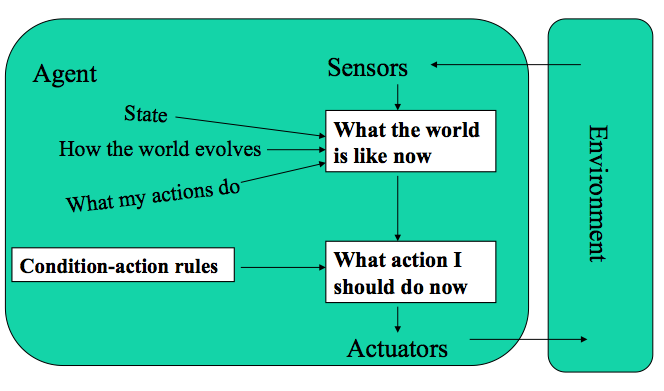
Requires keeping some "state" information.
Updating the state over time requires:
Search is a universal problem solving mechanism in AI. The sequence of steps required to solve a problem is not known a priori and it must be determined by a search exploration of alternatives.
Originated with Newell and Simon's work on problem solving. Famous book: "Human Problem Solving? (1972)"
In computer science, a state space is a description of a configuration of discrete states used as a simple model of machines. Formally, it can be defined as a tuple [N, A, S, G] where:
Often, there are oracles that offer clues on the current progress in the search
While "g(x)" can be known exactly (since it is a log of the past) while "h(x)" is a heuristic guess-timate (since we have not searched there yet).
The state space is what state space search searches in. Graph theory is helpful in understanding and reasoning about state spaces.
A state space has some common properties:
It is useful to distinguish two kinds of search:
Ordered search is useful for problems with some inherent ordering (e.g.) walking a maze.
Unordered search is useful for problems where ordering does not matter. For example, if a simulator accepts N inputs, then an unordered search might supply M ≤ N inputs and the rest are filled in at random.
In practice, S may not be pre-computed and cached. Rather, the successors to some state "s" may be computed using some "successors" function only when, or if, we ever reach "s". In the following code:
L = make-list(initial-state)
loop
node = remove-front(L) (node contains path of how we got there)
if goal-p(node) == true then
return(path to node)
S = successors (node)
combine (S,L)
until L is empty
return failure
Or, to say that another way...
(defun tree-search (states goal-p successors combiner)
(labels ((next () (funcall successors (first states)))
(more-states () (funcall combiner (next) (rest states))
(cond ((null states) nil) ; failure. boo!
((funcall goal-p (first states)) (first states)) ; success!
(t (tree-search ; more to do
(more-states) goal-p successors combiner))))
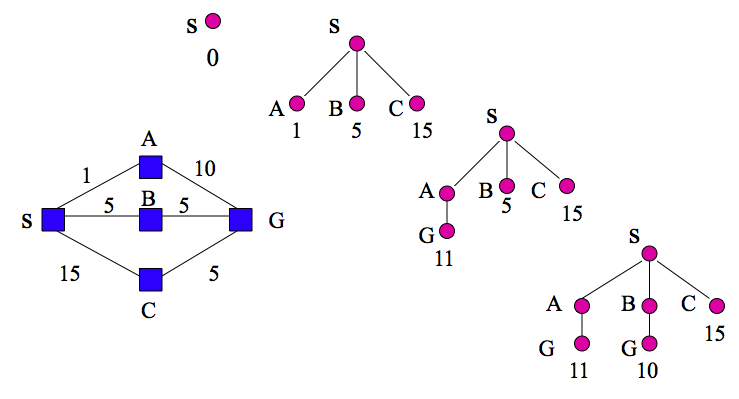
On execution, this generate a tree of search options. For example:
Question: what are the operators available at each step of the search?


Note the cycle down the left-hand branch of the tree.
Example: Monkey pushing a chair under a banana, climbs the chair, eats the banana. Recently solved by a pigeon:
(defparameter *banana-ops*
(list
(op 'climb-on-chair
:preconds '(chair-at-middle-room at-middle-room on-floor)
:add-list '(at-bananas on-chair)
:del-list '(at-middle-room on-floor))
(op 'push-chair-from-door-to-middle-room
:preconds '(chair-at-door at-door)
:add-list '(chair-at-middle-room at-middle-room)
:del-list '(chair-at-door at-door))
(op 'walk-from-door-to-middle-room
:preconds '(at-door on-floor)
:add-list '(at-middle-room)
:del-list '(at-door))
(op 'grasp-bananas
:preconds '(at-bananas empty-handed)
:add-list '(has-bananas)
:del-list '(empty-handed))
(op 'drop-ball
:preconds '(has-ball)
:add-list '(empty-handed)
:del-list '(has-ball))
(op 'eat-bananas
:preconds '(has-bananas)
:add-list '(empty-handed not-hungry)
:del-list '(has-bananas hungry))))
If the search space is small, then it is possible to write it manually (see above).
More commonly, the search space is auto-generated from some other representations (like the two examples that follow).
Here's walking a maze where "op" is inferred from the maze description:
(defparameter *maze-ops*
(mappend #'make-maze-ops
'((1 2) (2 3) (3 4) (4 9) (9 14) (9 8) (8 7) (7 12) (12 13)
(12 11) (11 6) (11 16) (16 17) (17 22) (21 22) (22 23)
(23 18) (23 24) (24 19) (19 20) (20 15) (15 10) (10 5) (20 25))))
(defun make-maze-op (here there)
"Make an operator to move between two places"
(op `(move from ,here to ,there)
:preconds `((at ,here))
:add-list `((at ,there))
:del-list `((at ,here))))
(defun make-maze-ops (pair)
"Make maze ops in both directions"
(list (make-maze-op (first pair) (second pair))
(make-maze-op (second pair) (first pair))))
(defun move-op (a b c)
"Make an operator to move A from B to C."
(op `(move ,a from ,b to ,c)
:preconds `((space on ,a) (space on ,c) (,a on ,b))
:add-list (move-ons a b c)
:del-list (move-ons a c b)))
(defun move-ons (a b c)
(if (eq b 'table)
`((,a on ,c))
`((,a on ,c) (space on ,b))))
(defun make-block-ops (blocks)
(let ((ops nil))
(dolist (a blocks)
(dolist (b blocks)
(unless (equal a b)
(dolist (c blocks)
(unless (or (equal c a) (equal c b))
(push (move-op a b c) ops)))
(push (move-op a 'table b) ops)
(push (move-op a b 'table) ops))))
ops))
General search methods to:
Evaluating a search strategy:
Consider all paths of length1, then length 2, then length3, then...

Let b = branching factor, d = solution depth, then the maximum number of nodes generated is:
Properties
This gets impractical, very quickly. Example:

Often, more states in our programs than stars in the sky (1024).
Like best: but only explores the top N ranked leaf items.
If infinite left-hand branches, then it will never backtrack to find solutions in right-hand-side branches.

Quite competitive, if the branching factor is large:
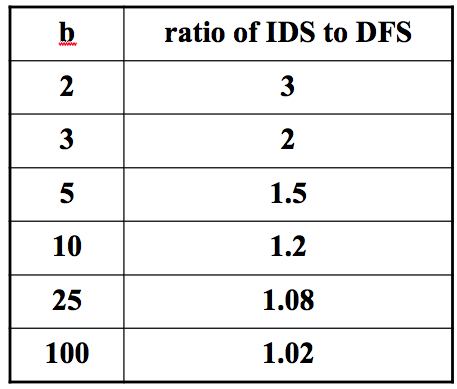
Same iterative widening methods can be applied to any search
For source code on the above, see here (to download this code, use http://unbox.org/wisp/var/timm/10/ai/doc/lisp/search.lisp).