2.2 Grammars

Syntax

• Syntax: the form or structure of the expressions, statements, and program units
• Semantics: the meaning of the expressions, statements, and program units

Definitions

• A "sentence" is a string of characters over some alphabet
• A "language" is a set of sentences
• A "lexeme" is the lowest level syntactic unit of a language (e.g., *, sum, begin)
• A "token" is a category of lexemes (e.g., identifier)

Context-Free Grammars

• Developed by Noam Chomsky in the mid-1950s
• Language generators, meant to describe the syntax of natural languages Define a class of languages called context-free languages

Backus-Naur Form (1959)

• Invented by John Backus to describe Algol 58
• BNF is equivalent to context-free grammars

Example:

<program> ==> <stmts>
  <stmts> ==> <stmt> | <stmt> ; <stmts>
   <stmt> ==> <var> = <expr>
   <var>  ==> a | b | c | d
   <expr> ==> <term> + <term> | <term> - <term>
   <term> ==> <var> | const

Example derivation:

<program> => <stmts>  => <stmt> 
                      => <var> = <expr> 
                      => a = <expr> 
                      => a = <term> + <term>
                      => a = <var> + <term> 
                      => a = b + <term>
                      => a = b + cons

Regular Expressions/

Specifies tokens. One of:

• A character
• The empty string, denoted ε
• Two regular expressions next to each other, meaning any string generated by the first one followed by (concatenated with) any string generated by the second one
• Two regular expressions separated by a vertical bar (|), meaning any string generated by the first one or any string generated by the second one
• A regular expression followed by a star "*", meaning the concatenation of zero or more strings generated by the expression in front of the star
• A regular expression followed by "?" meaning the concatenation of zero or one of strings generated by the expression in from of the "?"
• A regular expression followed by "+" meaning the concatenation of one or more of strings generated by the expression in from of the "+"

Parentheses are used to avoid ambiguity about where the various sub-expressions start and end.

Consider, for example, the syntax of numeric constants accepted by a simple hand-held calculator:

<number>   => <integer> | <real>
<integer>  => <digit> <digit> *
<real>     => <integer> <exponent> | <decimal> ( <exponent> | ε )
<decimal>  => <digit> * ( . <digit> | <digit> . ) <digit> *
<exponent> => ( e | E ) ( + | - | ε ) <integer>
<digit>    => 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

Finite State Automata

A regular expression can be viewed as a finite state automota (FSA) that recognizes (or generates) a valid sentence in a language.

• An FSA may be either deterministic (DFSA or DFA) or non-deterministic (NFSA or NFA).
• An FSA is deterministic if its behavior during recognition is fully determined by the state it is in and the symbol to be consumed. I.e., given an input string, only one path may be taken through the FSA.
• Conversely, an FSA is non-deterministic if, given an input string, more than one path may be taken through the FSA. One type of non-determinism is e-transitions, i.e. transitions which consume the empty string (no symbols).

FSAs can be represented as transitions between states

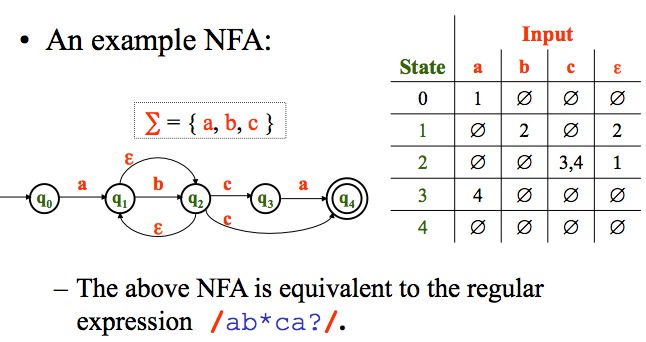
Parser generators build these state transition tables (so that subsequent processing a programming language is very fast).

Parse tree

A hierarchical representation of a derivation

                    <program>
                        |
                     <stmts>
                        |
                     <stmt>
                    /  |   \
                   /   |    \
                  /    |     \
              <var>   "="    <expr>
                |           /  |   \
              "a"     <term>  "+"   <term>
                        |             |
                      <var>         const
                        |
                       "b"

A grammar is "ambiguous" if and only if it generates a sentential form that has two or more distinct parse trees

• Example:

  <expr> ==> <expr> <op> <expr>  |  const
  <op>   ==> /  |  -
  

•                <expr>                      <expr>
                /   \   \                   /   |    \
               /     \   \                 /    |     \
  	  <expr>   <op>  <expr>    <expr>  <op>   <expr>
        /  |   \       \      |          |      |    |  \   \
       /   |    \       |     |          |      |    |   \    \
      /    |     \      |     |          |      |    |    \     \
  <expr> <op>  <expr>   |     |          |      |   <expr> <op> <expr>
    |      |     |      |     |          |      |      |     |     |
  const   "-"   const   "/"  const     const   "-"   const  "/"   const
  

Fix: If we use the parse tree to indicate precedence levels of the operators, we cannot have ambiguity

• Example:

  <expr> ==> <expr> - <term>  |  <term>
  <term> ==> <term> / const| const
  

•          <expr>
          /   |   \
     <expr>  "-"  <term>
        |         |  \  \
        |         |   \  \
        |         |    \  \
     <term>    <term> "/"  const
        |         |
     <const>   <const>
  

Operator associativity can also be indicated by a grammar

<expr> ==> <expr> + <expr> |  const  (ambiguous)
<expr> ==> <expr> + const  |  const  (unambiguous

Parse:

                 <expr>
                /  |   \
          <expr>  "+"   const
        /   |   \    
  <expr>   "+"   const 
     |
   const

Attributed Grammars

Grammars generate all properly formed expressions in some language but says nothing about their meaning. To tie these expressions to mathematical concepts we need additional notation.

The most common is based on attributes. In our expression grammar, we can associate a val attribute with each E, T, F, and const in the grammar.

The intent is that for any symbol S, S.val will be the meaning, as an arithmetic value, of the token string derived from S. We assume that the val of a const is provided to us by the scanner.

We must then invent a set of rules for each production, to specify how the vals of different symbols are related. The resulting attribute grammar (AG) for a simple calculator is shown here:

Object Grammars

Going one step further, the "Parse tree" is a nested set of objects. In this design, each non-terminal is some instance of sub-class of "Grammar". Once a language is parsed, an OO interpreter can execute the parse tree, with each non-terminal handling the specific processing associated with that node.

For example, an if-test would create and instance of class "If" with slots for "expr" and then "then" and "else" actions.

<if> => if <expr> then <action> else <action> fi

To interpret this, the OO interpreter just sends the message "evaluate" to this instance which, in turn, sends "evaluate" to "expr". If that returns true, then the "then" action is messaged with "evaluate". Else, we "evaluate" the "else".

This document was generated on April 19, 2011 using texi2html 5.0.