EECE 571F= Domain-Specific Languages  
  
This is a page from yet
another great ECE, UBC subject.
[ Home | Assignments | Lectures |
DSL rules | Articles | Resources ]

Abduction and DSLs

Lectures:
Old: 1 | 2 | 3 | 4 | 5
New: DCGnums | Parsing | Meta-prolog | Faster1 | Faster2 | Rand-nums
Not done: Abduction | Stochastic abs
With integrity, we can't advocate DSLs unless we also show that we can understand all these idiosyncratic languages.

So, how can this be done? What does "understanding" mean?

Informally: understanding a DSL = poke around it and see what it can do.

But this can produce too many conclusions. So lets impose a little restriction.

Restriction 1:

  • Define some goals.
  • Note: goals can be things we want to achieve OR things we wan't to avoid.
  • For stuff that effects those goals, poke around and see what happens.

Formally (v1): extract beliefs from the DSL assertions that lead to goals.

For many systems, we lack total knowledge.

  • So, sometimes during simulation, we'll have to guess at stuff we don't know.
  • "Guessing"= make assumptions.
So, formally (v2): extract consistent beliefs from the DSL assertions.

I.e. don't assume one thing about X here and the opposite thing about X over there.

Now,

Formally (v3):

  • Equation 1: Theory and Assumptions implies Goals.
  • Equation 2: Theory and Assumptions is an ok thing to do.

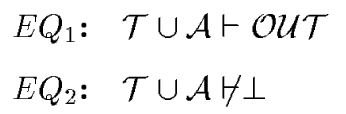
Formally, this is abduction.

Abduction: the details

Abduction= Make what inferences you can that are relevant to some goal (equation 1) without doing crazy things (equation 2).

Abduction is an astonishingly useful inference procedure- make what guesses you need to get to some goal but don't screw up along the way.

Known applications [Menzies, 1996]:

  • prediction,
  • classification,
  • explanation,
  • tutoring,
  • qualitative reasoning,
  • planning,
  • monitoring,
  • set-covering diagnosis,
  • consistency-based diagnosis
  • See [Kakas et.al. 1998] for other lists of applications of abduction.
Also, as we shall see, it is also good for validation; i.e. abduction we can implement both inference tools and testing tools.

Further, abduction can execute in vague and conflicting domains (which we believe occur very frequently).

Consistency

To define "inconsistency", we'll need some predicates defining "nogood". A standard definition is that we can't believe something and its negation: 


nogood(X,not X).
nogood(not X, X).

Another standard definition is that we can only assign one value to a variable: 


nogood(Var=Value1,Var=Value2) :- 
      not Value1 = Value2.

Another definition of consistent assignment we will use will be based on standard type definitions: 


:- [magic].

person= [name = string, age = age].

% which expands magically to...
% #person(Name,Age) :- #string(Name), #age(Age).
#age(Age) :- range(0,120,Age).
#string(X) :- anAtom(X).

range(Min,Max,Age) :- 
      var(Age),!, 
      Age is Min + round((Max-Min)*random(100)/99).
range(Min,Max,Age) :- number(Age), Min =< Age, Age =< Max.
anAtom(X)  :- var(X),!,gensym(x,X).
anAtom(X)  :- nonvar(X), atom(X).

BTW, here is the type definition magic. 


% magic.pl
:- op(999,fx,#).
:- op(800,xfx,are).
:- discontiguous (#)/1, def/2.
:- multifile     (#)/1, def/2.

term_expansion(A=L,[def(A,Fields),(#Head :- Body)]) :- 
    makeType(L,Body,Fields,Vars),
    Head =.. [A|Vars].

makeType([Field=Type],#Term,[Field],[Var]) :-
    Term =.. [Type,Var].
makeType([Field=Type,Next|Rest],(#Term,Terms),
     [Field|Fields],[Var|Vars]) :-
    Term =.. [Type,Var],
    makeType([Next|Rest],Terms,Fields,Vars).

If our theory can generate contradictions, then we can only use a subset of the theory to reach some subset of the goals: Formally (v4):

  • Equation 0a: Theory' = subset(Theory)
  • Equation 0b: Goals' = subset(Goal)
  • Equation 1': Theory' and Assumptions implies Goals'.
  • Equation 2': Theory' and Assumptions is an ok thing to do.
If can make up new ideas as we go, then "assumptions" can mean "add new knowledge". Pragmatically, this is much harder than just walk over existing knowledge, looking for useful bits. So, Restriction 2:
  • Equation 3: Assumptions = subset(Theory)
In "set-covering abduction", we only fret about the bits of the theory that lead from inputs to known goals. This will be king of abduction explored here. An alternative is "consistency-based abduction" in which assumptions are made for all variables, whether or not those variables are required to reach goals from inputs.

Worlds

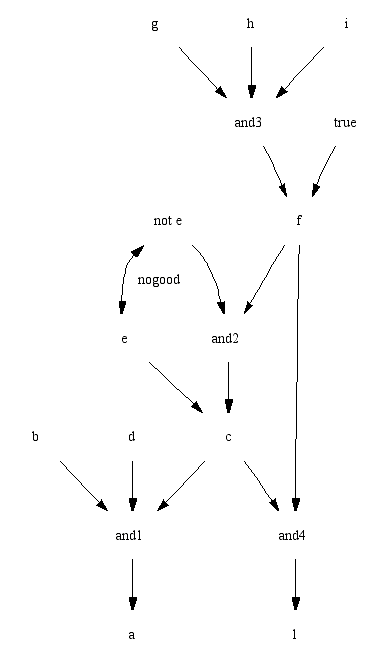
Since we are making assumptions, there may be alternate possible assumptions and more than one way to solve Equations 1-3. Each solution represents a different world of belief. Given the goal "a" in "proper.pl", there are three solutions to Equations 1-3. 


%proper.pl
a :- b , c , d.
c :- not  e, f.
c :- e.
f :- g, h, i.
f.
l :- c, f.

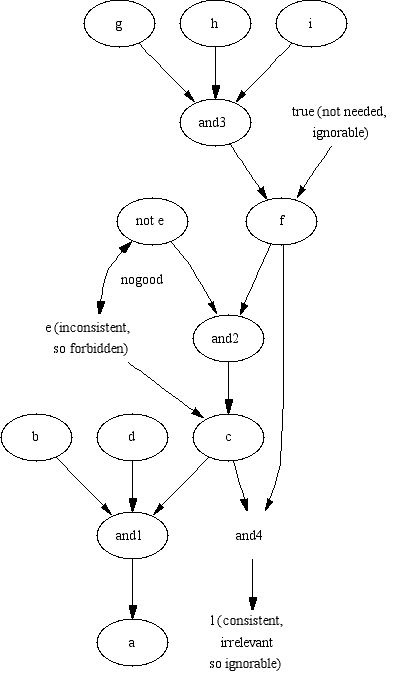
Assumptions = a, b, c, not e, f, g, h, i, d.

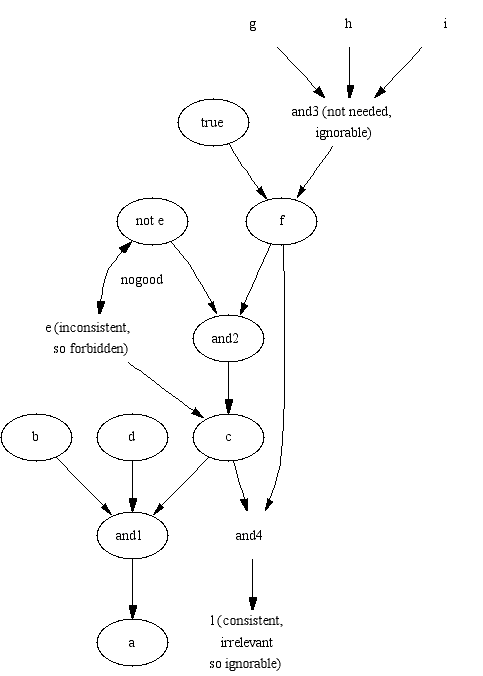
Assumptions = a, b, c, not e, f, d

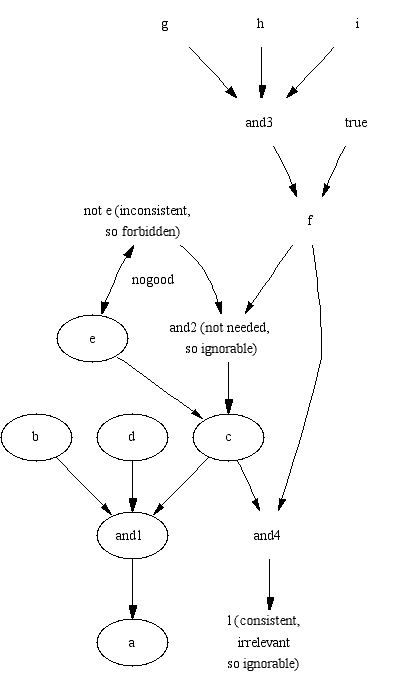
Assumptions = a, b, c, e, d

What is the "BEST" world?

So we have to add a "BEST" operator to select the preferred world(s).

  • E.g. cheapness: favor the smallest worlds (for least cost traversal)
  • E.g. certainty: favor the worlds that make the fewest assumptions
  • E.g. pleasure: favor worlds with the things we care about the most.
  • E.g. rudeness: don't favor worlds that contain things said by a known idiot.
  • E.g. diplomacy: favor worlds that contains a balance of things said by me and that idiot.
  • E.g. ...
No best "BEST"- a domain-specific operator that should be customizable.

Selection of "BEST" controls which worlds are reported and which task abduction is performing:

  • E.g. cheapness is best for least cost planning.
  • E.g. diplomacy is best for negotiation in requirements engineering
  • For more "BEST" operators, see [Menzies, 1996].
Customize "BEST", and you customize your DSL.
  • Ideally, "BEST" can be customized AFTER the domain facts are collected.
  • DSL user need not trouble themselves with procedural details of how their sentences will be traversed.

In any case, this leaves us with the following framework:

  • Users make assertions into their DSL.
  • Users specify goals.
  • DSL analysts customize BEST.
  • Worlds=solutions(Equations 1-3)
  • Best World(s)= BEST(Worlds)
  • Report best worlds.

The Bad News: Computational Cost

Equation 1 is like standard deduction. Given some premises (assumptions), we can reach some conclusions (goals).

Equation 2 is the runtime killer.

  • Deduction is a fast 100 meter sprint. Just run along without checking what you are doing. Bang! They are racing! Zap to the finish.
  • Abduction is like nervous accountants. After the "bang!", they shuffle forward a few inches then stop to nervously check if everything is ok.
  • Theories represented as horn clauses can be viewed a directed graph from sub-goals to clause heads.
  • Executing (e.g.) Prolog is like taking some out some paths over that graph.
  • Generating a consistent pathway across a directed graph containing incompatible (e.g. inconsistent) nodes is a NP-hard task [Gabow et.al. 1976].
  • That is, there exists no known complete abductive algorithm for quickly building such pathways.
  • Worse, the upper-bound on the runtime could be too slow: exponential on number of terms in a ground version of the horn clause theory.
  • Similar pessimistic comments can be found in [Bylander et.al. 1991, Selman & Levesque ]
  • Which is another way of saying that juggling lots of "what-ifs" is much harder than just committing to some idea, then power on unquestioningly.
  • So we'll have to address the complexity issue.

Stochastic Abduction

A bizarre observation is that the greatest number of goals reached in all worlds can be nearly equal to the number of goals reached in any world, picked at random [Menzies and Michael, 1999].

This observation was not just some quirk of the Menzies and Michael test domain. For example, in the testing literature, it has often been reported that a small number of probes often yields as much information as a much larger number of probes [Menzies and Cukic, 2000].

Further, simulations with an abstract model of searching a graph containing incompatible pairs suggest that the above empirical observations can be trusted as the expected case [Menzies and Cukic, 2000]..

This has lead to the speculation that, when probing a theory, a strategy that might work well is a limited number of random probes [Menzies and Cukic, 2002].

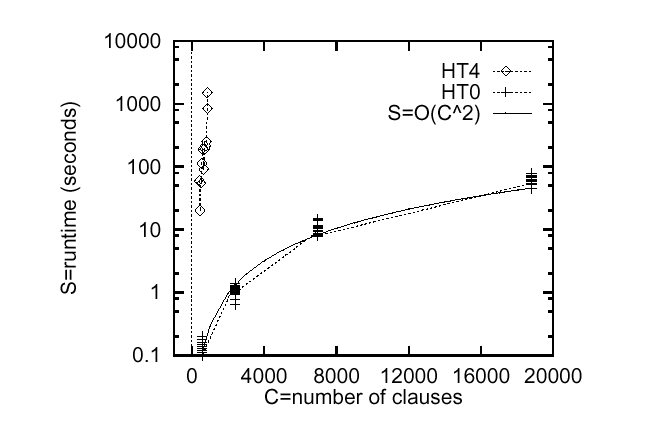
The advantage of this approach is faster runtimes. Numerous studies with stochastic search have been able to complete NP-hard tasks for very large theories (e.g. [Selman et.al. 1992]). Menzies and Michael [1996] found that a stochastic variant of an abductive inference engine could find 98% of the goals of a full abductive search, while running much faster:

One explanation for these bizarre results is "funnel theory":

  • Full worlds search and random worlds search achieve the same result since both are constrained by the same "funnel".
  • Funnel= a small number of variables within a theory set the values of the rest.
  • Any randomly selected pathway to goals must sample the funnel variables (by definition).
  • If the funnel is narrow, then a small number of random probes will be enough to sample all the funnel.
  • Funnel synonyms (many of which pre-date funnel theory):
    • prime implicant
    • shortest no-good
    • master-slave variables
    • ...
I.e. in many domains, it has been observed that a small part of the theory controls the rest.

So, we can exploit the funnel in the following ways:

  1. Assume it exists and see what you can find out about a theory.
    • If you don't find much, then move on to more elaborate analysis. In which case, you have wasted a little time.
    • If you do find out a lot, then you have saved yourself that more elaborate, slower, expensive, analysis.
  2. Use stochastic search in our abduction to sub-sample the possibilities.
  3. Easily build summaries of our sampling (just look for the variable ranges that occur at high frequency- these will be the funnel variables.
For more on points 2 and 3, see rest of this subject.
Not © Tim Menzies, 2001
Share and enjoy- information wants to be free.
But if you take anything from this site,
please credit tim@menzies.com.