Advanced Search
Learning Objectives:
- Explain what genetic algorithms are and contrast their effectiveness with the classic problem-solving
and search techniques.
- Explain how simulated annealing can be used to reduce search complexity and contrast its operation with
classic search techniques.
- Apply local search techniques to a classic domain.
Further reading:
Graph search
Like tree search, but
with a *visited* list that checks if some state has not been reached before.
Visited list can take a lot of memory
- Standard fix: some hashing scheme so that states get stored in a compact representation
- Incomplete: if different reached states happen to hash to the same value.
A* search: standard game playing technique:
-
Best-first search of graph with a *visited* list where states are sorted by "g+h"
- g(x)= Cost to reach state "x" from start
- h(x)= Heuristic estimate of cost to go from "x" to goal
- Important: h(x) must under-estimate cost from "x" to goal
- E.g. straight line "as the bird flies"
distance to shop at the Target store is less than the
actual driving distance
-
Once it has found a goal, then by definition, A* does not need to explore more nodes:
-
When A* terminates its search, it has, by definition, found a path whose actual cost is lower than the estimated cost of any path through any open node (assumption: h(x) over-estimates the distance).
- But since those estimates are optimistic, A* can safely ignore those nodes.
So A* will never overlook the possibility of a lower-cost path and so is admissible.
-
Suppose now that some other search algorithm B terminates its search with a path whose actual cost is not less than the estimated cost of a path through some open node:
-
Algorithm B cannot rule out the possibility, based on the heuristic information it has, that a path through that node might have a lower cost.
- So while B might consider fewer nodes than A*, it is tempting to keep exploring.
-
Accordingly, A* considers the fewest nodes of any admissible search algorithm that uses a no more accurate heuristic estimate.
Two-player Systems
So if the above methods are all standard, the enemy knows them too.
Q1: How can you reason about the enemy reasoning about your reasoning?
- A1: MinMax trees

Q2: How you do the above faster?
- A2: Alpha-Beta pruning.
Each node is shown with the [min,max] range. In general the [min,max] bounds become tighter and tighter as you proceed down the tree from the root.
Sometimes, you can skip a subtree if its min/max is out-of-bounds of the current min-max.
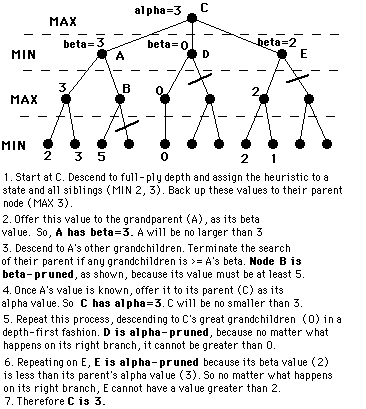
See http://www.ocf.berkeley.edu/~yosenl/extras/alphabeta/alphabeta.html
There is a common illusion that we first generate a n-ply minmax tree and then apply
alpha-beta prune. No, we generate the tree and apply alpha-beta prune at the same time
(otherwise, no point).
How effective is alpha-beta pruning? It depends on the order in which children are visited. If children of a node are visited in the worst possible order, it may be that no pruning occurs. For max nodes, we want to visit the best child first so that time is not wasted in the rest of the children exploring worse scenarios. For min nodes, we want to visit the worst child first (from our perspective, not the opponent's.) There are two obvious sources of this information:
-
A static evaluator function can be used to rank the child nodes
- Previous searches of the game tree (for example, from previous moves) performed minimax evaluations of many game positions. If available, these values may be used to rank the nodes.
When the optimal child is selected at every opportunity, alpha-beta
pruning causes all the rest of the children to be pruned away at
every other level of the tree; only that one child is explored.
This means that on average the tree can searched twice as deeply
as before: a huge increase in searching performance.
Stochastic Tree Search
ISAMP (iterative sampling)
- Start at "start".
- If too many restarts, stop.
- Take any successor.
- Repeat till
you hit a dead-end or "goal".
- If dead-end, then restart
This stochastic tree search can be readily adapted to other problem types.
Eg#1: scheduling problems
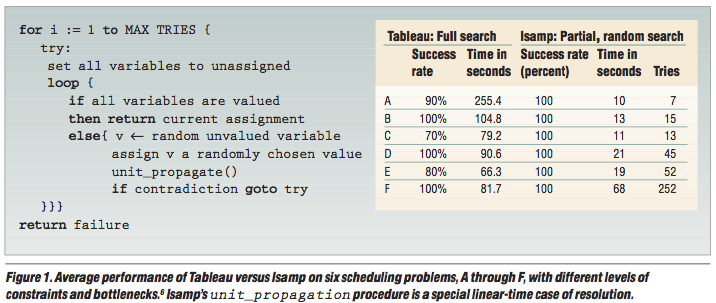
Eg#2: N-queens with the lurch
algorithm. From state "x", pick an out-arc at random. Follow it to some max depth.
Restart.
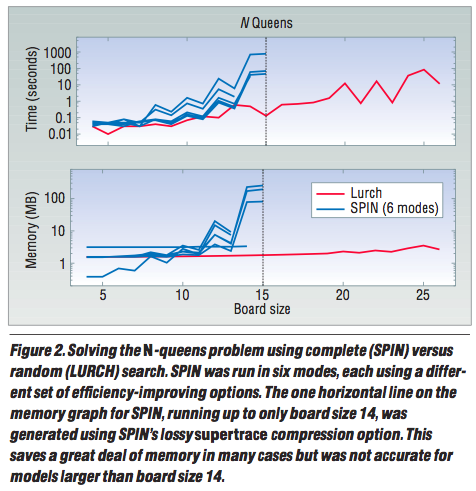
Note: subsequent research found numerous better variants of the at
IJCAI'95,
AAAI'96,
and
in 2002.
Q: Why does Isamp work so well. work so well?
- A: Few solutions, large space between them. Complete search wastes a lot of
time if it lucks into a poor initial set of choices.
Unordered searchers
Strangely, order may not matter. Rather than struggle with lots of tricky decisions,
- exploit speed of modern CPUs, CPU farms.
- try lots of possibilities, very quickly
For example:
- current := a random solution across the space
- If its better than anything seen so far, then best := current
Stochastic search: randomly fiddle with current solution
- Change part of the current solution at random
Local search: . replace random stabs with a little tinkering
- Change that part of the solution that most improves score
Some algorithms just do stochastic search (e.g. simulated annealing)
while others do both (MAXWALKSAT)
Simulated Annealing
S. Kirkpatrick and C. D. Gelatt and M. P. Vecchi
Optimization by Simulated Annealing, Science, Number 4598, 13 May 1983, volume 220, 4598, pages 671680,1983.
s := s0; e := E(s) // Initial state, energy.
sb := s; eb := e // Initial "best" solution
k := 0 // Energy evaluation count.
WHILE k < kmax and e > emax // While time remains & not good enough:
sn := neighbor(s) // Pick some neighbor.
en := E(sn) // Compute its energy.
IF en < eb // Is this a new best?
THEN sb := sn; eb := en // Yes, save it.
FI
IF random() > P(e, en, k/kmax) // Should we move to it?
THEN s := sn; e := en // Yes, change state.
FI
k := k + 1 // One more evaluation done
RETURN sb // Return the best solution found.
Note the space requirements for SA: only enough RAM to hold 3 solutions. Very
good for old fashioned machines.
But what to us for the probability function "P"? This is standard function:
FUNCTION P(old,new,t) = e^((old-new)/t)
Which, incidentally, looks like this:
-
Initially:
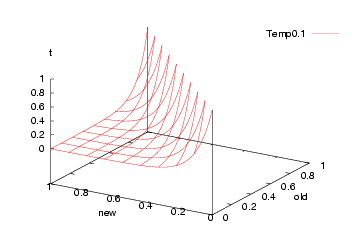
-
Subsequently:
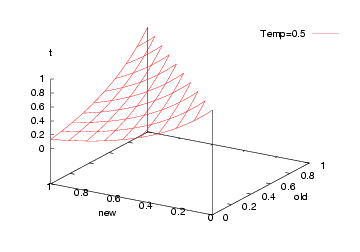
-
Finally:
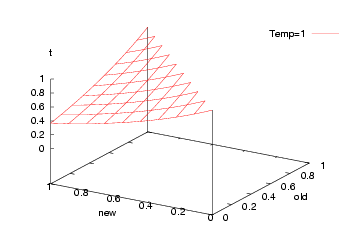
That is, we jump to a worse solution when "random() > P"
in two cases:
- The sensible case: if "new" is greater than "old"
- The crazy case: earlier in the run (when "t" is small)
Note that such crazy jumps let us escape local minima.
MAXWALKSAT
Kautz, H., Selman, B., & Jiang, Y.
A general stochastic approach to solving problems with hard and soft constraints. In D. Gu, J. Du and P. Pardalos (Eds.), The satisfiability problem: Theory and applications, 573586. New York, NY, 1997.
State of the art search algorithm.
FOR i = 1 to max-tries DO
solution = random assignment
FOR j =1 to max-changes DO
IF score(solution) > threshold
THEN RETURN solution
FI
c = random part of solution
IF p < random()
THEN change a random setting in c
ELSE change setting in c that maximizes score(solution)
FI
RETURN failure, best solution found
This is a very successful algorithm. Here's some performance of
WALKSAT (a simpler version of MAXWALKSAT) against a complete search
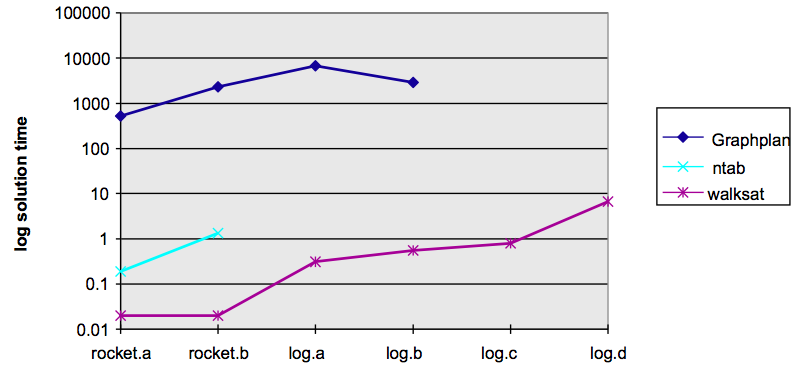
 You saw another example in the introduction to this subject.
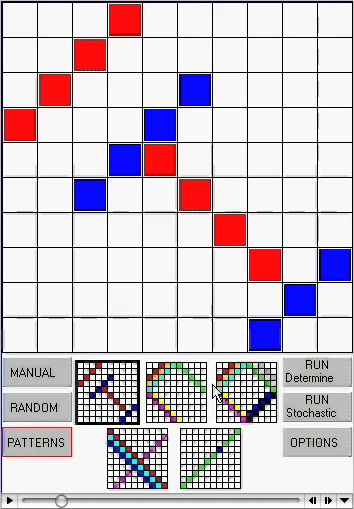
The movie at right shows two AI algorithms t$
solve the "latin's square" problem: i.e. pick an initial pattern, then try to
fill in the rest of the square with no two colors on the same row or column.
You saw another example in the introduction to this subject.
The movie at right shows two AI algorithms t$
solve the "latin's square" problem: i.e. pick an initial pattern, then try to
fill in the rest of the square with no two colors on the same row or column.
- The deterministic method is the kind of exhaustive theorem proving method
used in the 1960s and 1970s that convinced people that "AI can never work".
- The stochastic method is a 1990s-style AI algorithm that makes some
initial guess, then refines that guess based on logic feedback.
This stochastic
local search kills the latin squares problem (and, incidently, many other problems).
Genetic Algoirthms
GAs = mutate bit-strings
GPs = mutate parse trees of programs
The dream:
- Stop writing programs
- Instead, go and catch them
Take a herd of variants on a program
- Let them fight it out for a while
- Go fetch
GP= mutation of program structure
- Special form of GA (genetic algorithms)

GP selection
- Rank
- population is sorted according to objective values
- Roulette
- fitness increases chances of selection
- selection made probabilistically
- Elitism
- only the top N fittest carry over to next generation
- Stochastic Universal Sampling
- equal opportunity for all
Cross-over
Single point crossover (One random crossover point)
- 11001010101010101101 ⇒ 11001010i110011001101
- 10011001110011001101 ⇒ 10011001101010101101
Two point crossover (Two random crossover points)
- 11001010101010101101 ⇒ 11001001110011101101
- 10011001110011001101 ⇒ 10011010101010001101
Uniform crossover (Probabilistic bit selection)
- 11001010101010101101 ⇒ 11001001100011101101
- 10011001110011001101 ⇒ 10011010111010001101
Mutation: Randomly flip bits
Q: Why Mutate?
- A: Promotes diversity in the next generation.
Approaches
- Order changing: Swap 2 bits from a chromosome.
- 10011001110011001101 ⇒ 10010001110011011101
- Adding/Subtracting: Slight changes to real # encoding
- (1.12 3.65 3.86 4.31 5.21) ⇒ (1.12 3.65 3.73 4.23 5.21)
And why stop at bit strings?

Recommended Settings
All generalities are false. But, just to get you started:
- Population size: 50
- Number of generations: 1,000
- Crossover type: typically two point
- Crossover rate: 60%
- Mutation type: bit flip
- Mutation rate: 0.001
GP as automated invention machines
Koza, John R., Keane, Martin A., and Streeter, Matthew J. 2003c. i
What's AI done for me lately? Genetic programming's
human-competitive results IEEE Intelligent Systems. Volume 18. Number 3. May/June 2003. Pages 25-31.
Automatic synthesis of computer programs for 21 "human-competitive",
previously patented inventions:

Koza lists 36 "human-competitive" results (including the above patents):
- The result was patented as an invention in the past,is an improvement over a patented invention,or would qualify today as a patentable new invention.
- The result is equal to or better than a result that
was accepted as a new scientific result at the
time when it was published in a peer-reviewed
scientific journal.
- The result is equal to or better than a result that
was placed into a database or archive of results
maintained by an internationally recognized
panel of scientific experts.
- The result is publishable in its own right as a
new scientific result independent of the fact
that the result was mechanically created.
- The result is equal to or better than the most
recent human-created solution to a long-standing problem for which there has been a succession of
increasingly better human-created
solutions.
- The result is equal to or better than a result that
was considered an achievement in its field
when it was first discovered.
- The result solves a problem of indisputable difficulty in its field.
- The result holds its own or wins a regulated
competition involving human contestants (in
the form of either live human players or human-written computer programs).










 You saw another example in the introduction to this subject.
The movie at right shows two AI algorithms t$
solve the "latin's square" problem: i.e. pick an initial pattern, then try to
fill in the rest of the square with no two colors on the same row or column.
You saw another example in the introduction to this subject.
The movie at right shows two AI algorithms t$
solve the "latin's square" problem: i.e. pick an initial pattern, then try to
fill in the rest of the square with no two colors on the same row or column.



