
| [ << ] | [ < ] | [ Up ] | [ > ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
This subject is about inhuman AI, all the tricks that computers can use to be smart that humans may or may not use.
Just to give the humans’ a little more equality in this subject, today were going to talk about humans and AI. The field of cognitive science is devoted to discovering more about human intelligence using insights from a range of other areas including:
Human brain cells are very different to computer chips. In your brain, there is:


A nerve cell can have up to 1000 dendritic branches, making connections with tens of thousands of other cells. Each of the 10^11 (one hundred billion) neurons has on average 7,000 connections to other neurons.
It has been estimated that the brain of a three-year-old child has about 10^16 synapses (10 quadrillion). This number declines with age, stabilizing by adulthood. Estimates vary for an adult, ranging from 10^15 to 5 x 10^15 synapses (1 to 5 quadrillion).
Just to say the obvious- that’s a BIG network.
Neuro-physiology is a very active field. The latest generation of MRI scanners allow for detailed real-time monitoring of human activity, while they are performing cognitive tasks.
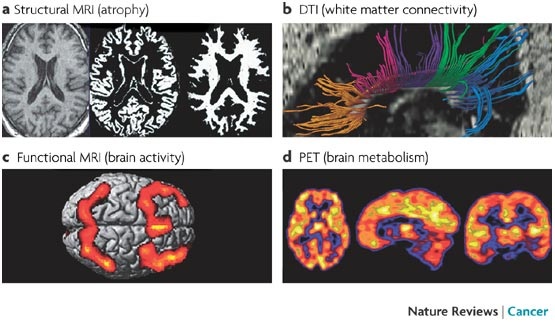
This field shows great promise but, as yet, they are still working on locomotion and pain perception and vision and have yet to rise to the level of model-based reasoning.
The field of neural networks originally began as an experiment in exploiting massive repetition of a single simple structure, running in parallel, to achieve cognition. As the field evolved, it turned more into some curve fitting over non-linear functions (and the tools used to achieve that fit have become less and less likely to have a biological correlate).
For another example of AI research, initially inspired by a biological metaphor, see genetic algorithms.
Noam Chomsky is one the towering figures of the 20th century. He’s a linguistic and a political commentator. Every few years he disappears to re-emerge with a new book the redefines everything. For example, a lot of computer science parsing theory comes from Chomsky’s theory of language grammars.
In AI circles, Chomsky is most famous for his argument that we don’t learn language. Rather, we are born with a general grammar and , as a child grows all up, all they are doing is filling some empty slots referring to the particulars of the local dialect.
This must be so, argues Chomsky otherwise language acquisition would be impossible.
The implications are staggering. Somewhere in the wet-ware of the brain there is something like the grammars we process in computer science. At its most optimistic, this also means that grammar-based languages (like LISP, etc) have what it takes to reproduce human cognition. We’ll return to this below (when we talk about the "physical symbol system hypothesis").

But is there really a "language" of thought? Or is this just an interpretation of chemicals sloshing around the dendrites (under the hood) which we interpret as language.
Well, there is evidence of some model-based manipulation by our wet ware. In classic mental rotation experiments, it was shown that the time required to check if some object was rotation of another was linear proportional to the size of the rotation. It is as if some brain box is reaching out to a sculpture of the thing we are looking at, the turning it around at some fixed rate.

Anyway, if ask a philosopher, "is it really neurons, or are their symbolic models in between our ears?", they might answer who cares?. Whatever stance works best is the right one.
Daniel Dennett asks a simple questions. Try and beat a chess playing program. What are you going to do?
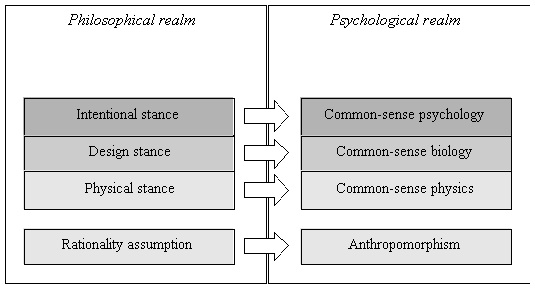
Which is the right stance? The answer is, it depends. What do you want to do? Stop being short circuited by a loose wire? You want the physical stance? Beat the program at chess? You want the intentional stance.
Bottom line: a computer is not just "a machine". It is a mix of things, some of which are best treated like any other intelligence.
Don’t believe me? Well, pawn to king four and may the best stance win.
(By the way, for a good introduction to AI and philosophy, see The Mind’s I).
I think therefore I am. I don’t think therefore...
There used to be a savage critic by certain philosophers along the lines that AI was impossible. For example, John Searle is a smart guy. His text Speech Acts: An Essay in the Philosophy of Language. 1969 is listed as one of the most cited works on the 20th century.
In one of the most famous critiques of early AI, Searle invented the Chinese Room: an ELIZA-like AI that used simple pattern look ups to react to user utterances. Searle argued that this was nonsense- that such a system could never be said to be "really" intelligent.

Looking back on it all, 27 years later, the whole debate seems wrong-headed. Of course ELIZA was the wrong model for intelligence- no internal model that is refined during interaction, no background knowledge, no inference, no set of beliefs/desires/goals, etc.

Searle’s argument amounts to "not enough- do more". And we did. Searle’s kind of rhetoric (that AI will never work) fails in the face of AI’s many successes.
Here’s some on-line resources on the topic:
And here’s some more general links:

There is some mathematical support for Searle’s pessimism. In 1930, the philosophical world was shaken to its foundation in 1930 by a mathematical paper that proved:
That is, formal systems have fundamental limits.
So Godel’s theorem gives us an absolute limit to what can be achieved by "formal systems" (i.e. the kinds of things we can write with a LISP program).
Godel’s theorem might be used to argue against the "logical school" of AI. If formal logics are so limited, then maybe we should ignore them and try other procedural / functional representations instead:
BTW, I do not regard Godel’s theorem as a limit to current research. I don’t know the length of my 1000th hair above my right ear but I can still buy a house, write programs, balance my check book, etc. So Godel’s theorem does not make me want to junk my LISP compiler and go off into procedural neural net land.
Godel’s theorem is somewhat arcane. He showed that some things were unknowable but he did not say what those things are.
Enter Steve Cook. In 1971, he showed that commonly studied problems (e.g. boolean satisfiability) belong to a class of systems for which the solution takes exponential time to compute.
An army of algorithms researchers have followed Cook’s lead and now there are vast catalogues of commonly studied programs for which there is no known fast (less than exponential time) and complete (no heuristic search) solution.
BTW, Cook showed that there exist algorithms that can’t implement a complete and fast solution to a wide range of problems. But neither can people. And (using stochastic search) we can get pretty good solutions pretty fast, even from pretty big problems.
O.K., so formal systems can never be omniscient, but how good do you have to be to "as smart as humans"?
The answer is, sometimes, not very smart at all. The cognitive psychology literature is full of examples where humans repeatedly reason in characteristic sub-optimal ways (see the wonderful Wikipedia page listing 35 decision-making biases and 28 biases in probability and belief and 20 social biases and 7 memory errors).
In fact, one the early successes of AI was not replicated some human cognitive skills, but also human cognitive failings. In the 1970s, AI researchers adopted the physical symbol system hypothesis:
A physical symbol system has the necessary and sufficient means of general intelligent action.
Here, by physical symbol system they mean
the basic processes that a computer can perform with symbols are to input them into memory, combine and reorganize them into symbol structures, store such structures over time,. . . .compare pairs of symbols for equality or inequality, and "branch" (behave conditionally on the outcome of such tests)
(Note that tacit in this hypothesis is Chomsky’s language of thought and the notion that computers can think like people if they can push around symbols, just like the brain.) Rule-based programs designed around this hypothesis could replicate not just feats of human comprehension, but also human inadequacies in the face of (e.g.) limited short term memory or immature long-term memory (see Expert and Novice Performance in Solving Physics Problems, Science, 1980 Jun 20;208(4450):1335-1342 Larkin J, McDermott J, Simon DP, Simon HA).
The AI work did not come in isolation. The physical symbol system hypothesis, for example, owed much to decades of psychological research. In particular, the cognitive psychology research that evolved as a reaction to behaviorism (from the early part of the 20th century). In its most extreme view, behaviorism denied all internal states and allowed for only the objective study of externally observable behavior (i.e. no mental life, no internal states; thought is covert speech).
Well, that flew for a few decades then it just ran out of steam. After decades of trying to map human behavior into (what seems now) trite stimulus response models, cognitive psychology made the obvious remark that the same input yields different outputs from different people because of their internal models. That is, intelligence is not just a reaction to the world. Rather, it is the careful construction and constant review of a set of internal states of belief which we use to decide how to best act next.
(Reference: Science, 20 June 1980, Vol. 208. no. 4450, pp. 1335 - 1342 "Expert and Novice Performance in Solving Physics Problems", Jill Larkin, John McDermott, Dorothea P. Simon, and Herbert A. Simon. )
Much of the early AI research was informed by a cognitive psychology model of human expertise. The model has two parts:
Reasoning was, according to this mode: a match-act cycle:
In this model
Q: How to experts know what is relevant?
A: feature extractors- gizmos that experts learn to let them glance at a situation and extract the salient details. E.g. chess experts can reproduce form memory all the positions on a chess board But if you show the same experts a gibberish game (one where all the rules are broken- e.g white pawns on white’s back row) then they can’t reproduce the board. Why? Well, when they glance at a board, their feature extractors fire to offer them a succinct summary. Gibberish boards baffle the feature extractors, so no summary
We study AI to learn useful tricks. Sometimes, we also learn something about people. Here’s a radically different, and successful, method to the above. What does it tell us about human cognition?
Ripple-down rules is a maintenance technique for rule-based programs initially developed by Compton. Ripple-down rules are best understood by comparison with standard rule-based programming. In standard rule-based programming, each rule takes the form
rule ID IF condition THEN action
where condition is some test on the current case. In the 1970s and early 1980s rule-based systems were hailed as the cure to the ills of software and knowledge engineering. Rules are useful, it was claimed, since they: represent high-level logic of the system expressed in a simple form that can be rapidly modified.
However, as these systems grew in size, it became apparent that rules were surprisingly harder to manage. One reason for this was that, in standard rule-based programming, all rules exist in one large global space where any rule can trigger any other rule. Such an open architecture is very flexible. However, it is also difficult to prevent unexpected side-effects after editing a rule. Consequently, the same rule-based programs hailed in early 1980s (XCON) became case studies about how hard it can be to maintain rule-based systems.
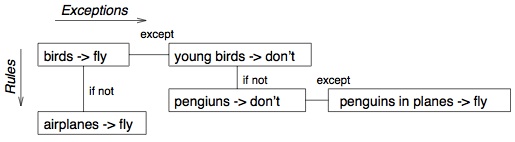
Many researchers argued that rule authors must work in precisely constrained environments, lest their edits lead to spaghetti knowledge and a maintenance nightmare. One such constrained environment is ripple-down rules that adds an EXCEPT slot to each rule:
rule ID1 IF condition THEN EXCEPT rule ID2 THEN conclusion because EXAMPLE
Here, ID1,ID2 are unique identifiers for different rules; EXAMPLE is the case that prompted the creation of the rule (internally, EXAMPLEs conjunction of features); and the condition is some subset of the EXAMPLE, i.e., condition ⊆ EXAMPLE (the method for selecting that subset is discussed below). Rules and their exceptions form a ripple-down rule tree:
At run time, a ripple-down rule interpreter explores the rules and their exceptions. If the condition of rule ID1 is found to be true, the interpreter checks the rule referenced in the except slot. If ID2’s rule condition is false, then the interpreter returns the conclusion of ID1. Else, the interpreter recurses into rule ID2.
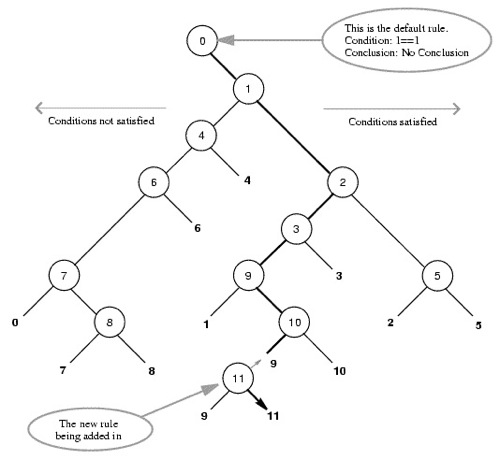
(Note the unbalanced nature of the tree, most patches are shallow. This is a common feature of RDRs).
Ripple-down rules can be easier to read than normal rules:

But in practice, Compton advises hiding the tree behind a difference-list editor. Such an editor constrains rule authoring as follows:
condition2 = EXAMPLE1 - condition1 condition2 ⊆ EXAMPLE2
When users work in a difference list editor, they watch EXAMPLEs running over the ripple-down rules tree, intervening only when they believe that the wrong conclusion is generated. At that point, the editor generates a list of features to add to condition2 (this list is generated automatically from the above equations). The expert picks some items from this list and the patch rule is automatically to some leaf of the ripple-down rules tree.
Ripple-down rules are a very rapid rule maintenance environment. Compton et.al. report average rule edit times between 30 to 120 seconds for rule bases up to 1000 rules in size [Compton 2005]
AFAIK, ripple-down-rules are the current high-water mark in knowledge maintenance.
Q: what does this tell us about human knowledge?
| [ << ] | [ < ] | [ Up ] | [ > ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
This document was generated on March 1, 2011 using texi2html 5.0.