2.4 Basic Search

Search is a universal problem solving mechanism in AI. The sequence of steps required to solve a problem is not known a priori and it must be determined by a search exploration of alternatives.

Originated with Newell and Simon’s work on problem solving. Famous book: "Human Problem Solving? (1972)"

• Automated reasoning is a natural search task
• More recently: Given that almost all AI formalisms (planning, learning, etc.) are NP-complete or worse, some form of search is generally unavoidable (no "smarter" algorithm available).

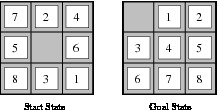
In computer science, a state space is a description of a configuration of discrete states used as a simple model of machines. Formally, it can be defined as a tuple [N, A, S, G] where:

• S is a nonempty subset of N that contains start states
• G is a nonempty subset of N that contains the goal states.
• N is a set of states, each with "successors"
• A is a set of arcs connecting each state to its successors

Often, there are oracles that offer clues on the current progress in the search

• g(x) is a measure of "distance" of state "x" from start.
• h(x) is a measure of "cost" required to get from state "x" to the goal.

While "g(x)" can be known exactly (since it is a log of the past) while "h(x)" is a heuristic guess-timate (since we have not searched there yet).

The state space is what state space search searches in. Graph theory is helpful in understanding and reasoning about state spaces.

A state space has some common properties:

• complexity, where branching factor "b" is important
• structure of the space, see also graph theory:
  • directionality of arcs
  • tree
  • rooted graph

It is useful to distinguish two kinds of search:

• Ordered-search; e.g. the tree and graph searchers discussed below. In this kind of search, the solutions spreads out in a wave over over some solution space.
• Unordered-search where a partial solution is quickly (?randomly) generated, then maybe fiddled with. A common unordered search method is to generate a number of slots, each with random values as done in simulated annealing or MAXWALKSAT (discussed below).

Ordered search is useful for problems with some inherent ordering (e.g.) walking a maze.

Unordered search is useful for problems where ordering does not matter. For example, if a simulator accepts N inputs, then an unordered search might supply M ≤ N inputs and the rest are filled in at random.

Problem Search Strategies

In practice, S may not be pre-computed and cached. Rather, the successors to some state "s" may be computed using some "successors" function only when, or if, we ever reach "s". In the following code:

• Some "goal-p" function checks if we have arrived at our goal.
• Some "combiner" function joins the successors with the rest of the states (maybe removing duplicates).

L = make-list(initial-state)
loop
   node = remove-front(L) (node contains path of how we got there)
   if goal-p(node) == true then
      return(path to node)
   S = successors (node)
   combine (S,L)
until L is empty
return failure

Or, to say that another way...

(defun tree-search (states goal-p  successors combiner)
  (labels ((next  ()       (funcall successors (first states)))
           (more-states () (funcall combiner   (next) (rest states))

   (cond ((null states) nil)                              ; failure. boo!
         ((funcall goal-p (first states)) (first states)) ; success!
         (t  (tree-search                                 ; more to do
               (more-states) goal-p successors combiner))))

• Devise a representation scheme for states
• Describe an initial and a final state
• Describe operators
• Select which state to expand next
• Recognize the goal when generated

Example: Tic Tac Toe

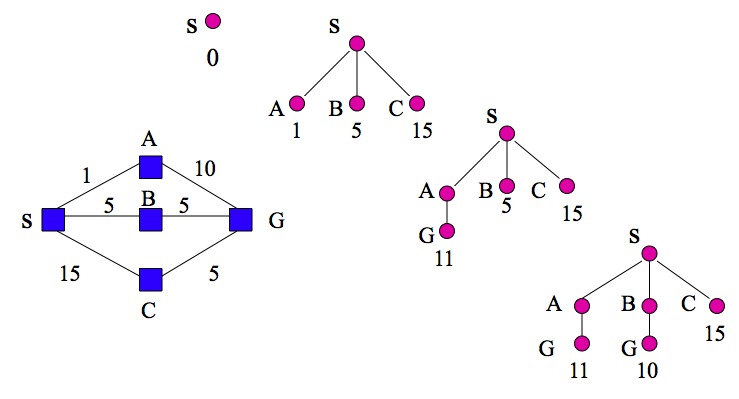
On execution, this generate a tree of search options. For example:

Question: what are the operators available at each step of the search?

Example: The 8 Puzzle

Note the cycle down the left-hand branch of the tree.

Getting the Banana

Example: Monkey pushing a chair under a banana, climbs the chair, eats the banana. Recently solved by a pigeon.

(defparameter *banana-ops*
  (list
    (op 'climb-on-chair
        :preconds '(chair-at-middle-room at-middle-room on-floor)
        :add-list '(at-bananas on-chair)
        :del-list '(at-middle-room on-floor))
    (op 'push-chair-from-door-to-middle-room
        :preconds '(chair-at-door at-door)
        :add-list '(chair-at-middle-room at-middle-room)
        :del-list '(chair-at-door at-door))
    (op 'walk-from-door-to-middle-room
        :preconds '(at-door on-floor)
        :add-list '(at-middle-room)
        :del-list '(at-door))
    (op 'grasp-bananas
        :preconds '(at-bananas empty-handed)
        :add-list '(has-bananas)
        :del-list '(empty-handed))
    (op 'drop-ball
        :preconds '(has-ball)
        :add-list '(empty-handed)
        :del-list '(has-ball))
    (op 'eat-bananas
        :preconds '(has-bananas)
        :add-list '(empty-handed not-hungry)
        :del-list '(has-bananas hungry))))

If the search space is small, then it is possible to write it manually (see above).

More commonly, the search space is auto-generated from some other representations (like the two examples that follow).

Maze

Here’s walking a maze where "op" is inferred from the maze description:

(defparameter *maze-ops*
  (mappend #'make-maze-ops
     '((1 2) (2 3) (3 4) (4 9) (9 14) (9 8) (8 7) (7 12) (12 13)
       (12 11) (11 6) (11 16) (16 17) (17 22) (21 22) (22 23)
       (23 18) (23 24) (24 19) (19 20) (20 15) (15 10) (10 5) (20 25))))

(defun make-maze-op (here there)
  "Make an operator to move between two places"
  (op `(move from ,here to ,there)
      :preconds `((at ,here))
      :add-list `((at ,there))
      :del-list `((at ,here))))

(defun make-maze-ops (pair)
  "Make maze ops in both directions"
  (list (make-maze-op (first pair) (second pair))
        (make-maze-op (second pair) (first pair))))

Blocks World

Here’s stacking some boxes till they get into some desired order.

(defun move-op (a b c)
  "Make an operator to move A from B to C."
  (op `(move ,a from ,b to ,c)
      :preconds `((space on ,a) (space on ,c) (,a on ,b))
      :add-list (move-ons a b c)
      :del-list (move-ons a c b)))

(defun move-ons (a b c)
  (if (eq b 'table)
      `((,a on ,c))
      `((,a on ,c) (space on ,b))))

(defun make-block-ops (blocks)
  (let ((ops nil))
    (dolist (a blocks)
      (dolist (b blocks)
        (unless (equal a b)
          (dolist (c blocks)
            (unless (or (equal c a) (equal c b))
              (push (move-op a b c) ops)))
          (push (move-op a 'table b) ops)
          (push (move-op a b 'table) ops))))
    ops))

Search Trees

General search methods to:

• Explore to depth "d"
• A tree that branches at a rate of "b" out-arcs per node

Evaluating a search strategy:

• Completeness: Is the strategy guaranteed to find a solution when there is one?
• Time Complexity: How long does it take to find a solution?
• Space Complexity: How much memory does it need?
• Optimality: Does strategy always find a lowest-cost path to solution? (this may include different cost of one solution vs. another).

Breadth-first search

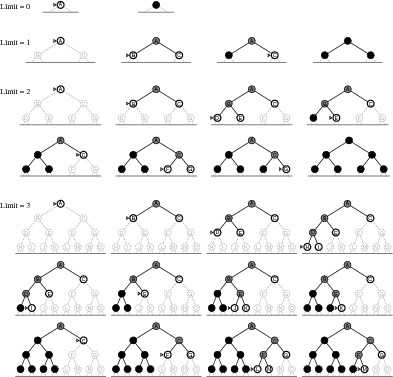
Consider all paths of length1, then length 2, then length3, then...

Let b = branching factor, d = solution depth, then the maximum number of nodes generated is:

• b + b2 + ... + bd + (bd+1-b) = O(bd+1)

Properties

• running time O(bd+1)
• most space: space requirements O(bd+1)
• least cost: (shortest path to the goal)

This gets impractical, very quickly. Example:

• b = 10
• 10000 nodes/second
• each node requires 1000 bytes of storage

Often, more states in our programs than stars in the sky (1024).

Best-first search

• Use BFS, but always expand the lowest-cost node on the fringe as measured by path cost g(n).
• Assumes that we have a good "g"; i.e. g(Successor(n)) ≥ g(n)

Beam search

Like best: but only explores the top N ranked leaf items.

• Only expand the "N" best ones
• Keep N small (10 or 20) to constrain search size.
• Note: small beams mean less memory but make the search incomplete (may miss solutions).

Depth first search

• running time O(b^d)
• least space: O(b * d)
  • At most, one branch from root to a leaf, knowing that there are "b" options per node.
  • may not find the minimum cost solution

  If infinite left-hand branches, then it will never backtrack to find solutions in right-hand-side branches.

DFID: depth-first iterative deepening

• Depth search to maximum depth Max
• Repeat for Max+1
• running time O(b^d)
• space requirements O(b*d)
• finds the minimum cost solution (shortest path to the goal)

Quite competitive, if the branching factor is large:

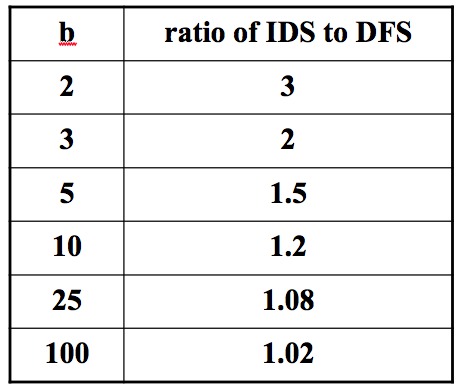
Same iterative widening methods can be applied to any search

Bidirectional search: hands across the water

• add a "precursors" function that returns parents of the current state (i.e. the opposite to "successors").
• Run two searches (forwards and backwards) it they ever meet, stop

This document was generated on March 1, 2011 using texi2html 5.0.